Exploiting Uncertainty for Querying Inconsistent Description Logics Knowledge Bases

The necessity to manage inconsistency in Description Logics Knowledge Bases (KBs) has come to the fore with the increasing importance gained by the Semantic Web, where information comes from different sources that constantly change their content and may contain contradictory descriptions when considered either alone or together. Classical reasoning algorithms do not handle inconsistent KBs, forcing the debugging of the KB in order to remove the inconsistency. In this paper, we exploit an existing probabilistic semantics called DISPONTE to overcome this problem and allow queries also in case of inconsistent KBs. We implemented our approach in the reasoners TRILL and BUNDLE and empirically tested the validity of our proposal. Moreover, we formally compare the presented approach to that of the repair semantics, one of the most established semantics when considering DL reasoning tasks.

Non-ground Abductive Logic Programming with Probabilistic Integrity Constraints

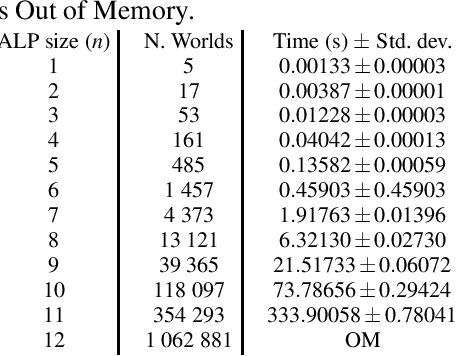
Uncertain information is being taken into account in an increasing number of application fields. In the meantime, abduction has been proved a powerful tool for handling hypothetical reasoning and incomplete knowledge. Probabilistic logical models are a suitable framework to handle uncertain information, and in the last decade many probabilistic logical languages have been proposed, as well as inference and learning systems for them. In the realm of Abductive Logic Programming (ALP), a variety of proof procedures have been defined as well. In this paper, we consider a richer logic language, coping with probabilistic abduction with variables. In particular, we consider an ALP program enriched with integrity constraints `a la IFF, possibly annotated with a probability value. We first present the overall abductive language, and its semantics according to the Distribution Semantics. We then introduce a proof procedure, obtained by extending one previously presented, and prove its soundness and completeness.

A Framework for Reasoning on Probabilistic Description Logics

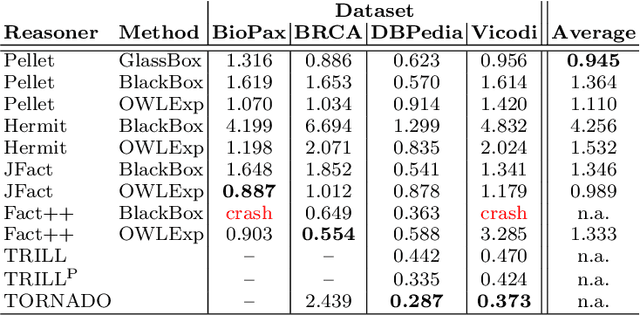
While there exist several reasoners for Description Logics, very few of them can cope with uncertainty. BUNDLE is an inference framework that can exploit several OWL (non-probabilistic) reasoners to perform inference over Probabilistic Description Logics. In this chapter, we report the latest advances implemented in BUNDLE. In particular, BUNDLE can now interface with the reasoners of the TRILL system, thus providing a uniform method to execute probabilistic queries using different settings. BUNDLE can be easily extended and can be used either as a standalone desktop application or as a library in OWL API-based applications that need to reason over Probabilistic Description Logics. The reasoning performance heavily depends on the reasoner and method used to compute the probability. We provide a comparison of the different reasoning settings on several datasets.

Automatic Setting of DNN Hyper-Parameters by Mixing Bayesian Optimization and Tuning Rules

Deep learning techniques play an increasingly important role in industrial and research environments due to their outstanding results. However, the large number of hyper-parameters to be set may lead to errors if they are set manually. The state-of-the-art hyper-parameters tuning methods are grid search, random search, and Bayesian Optimization. The first two methods are expensive because they try, respectively, all possible combinations and random combinations of hyper-parameters. Bayesian Optimization, instead, builds a surrogate model of the objective function, quantifies the uncertainty in the surrogate using Gaussian Process Regression and uses an acquisition function to decide where to sample the new set of hyper-parameters. This work faces the field of Hyper-Parameters Optimization (HPO). The aim is to improve Bayesian Optimization applied to Deep Neural Networks. For this goal, we build a new algorithm for evaluating and analyzing the results of the network on the training and validation sets and use a set of tuning rules to add new hyper-parameters and/or to reduce the hyper-parameter search space to select a better combination.

Probabilistic DL Reasoning with Pinpointing Formulas: A Prolog-based Approach

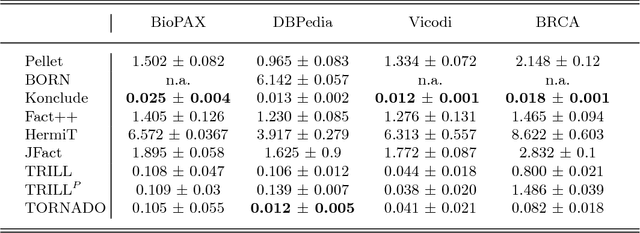
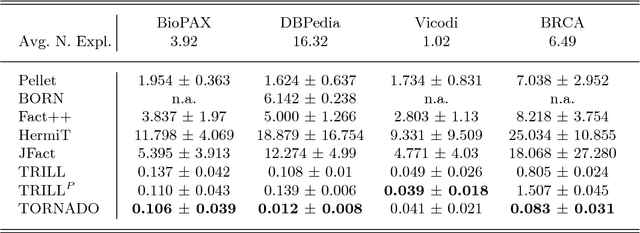
When modeling real world domains we have to deal with information that is incomplete or that comes from sources with different trust levels. This motivates the need for managing uncertainty in the Semantic Web. To this purpose, we introduced a probabilistic semantics, named DISPONTE, in order to combine description logics with probability theory. The probability of a query can be then computed from the set of its explanations by building a Binary Decision Diagram (BDD). The set of explanations can be found using the tableau algorithm, which has to handle non-determinism. Prolog, with its efficient handling of non-determinism, is suitable for implementing the tableau algorithm. TRILL and TRILLP are systems offering a Prolog implementation of the tableau algorithm. TRILLP builds a pinpointing formula, that compactly represents the set of explanations and can be directly translated into a BDD. Both reasoners were shown to outperform state-of-the-art DL reasoners. In this paper, we present an improvement of TRILLP, named TORNADO, in which the BDD is directly built during the construction of the tableau, further speeding up the overall inference process. An experimental comparison shows the effectiveness of TORNADO. All systems can be tried online in the TRILL on SWISH web application at http://trill.ml.unife.it/.

Lifted Variable Elimination for Probabilistic Logic Programming

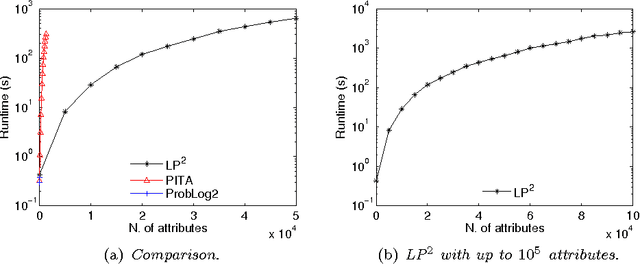
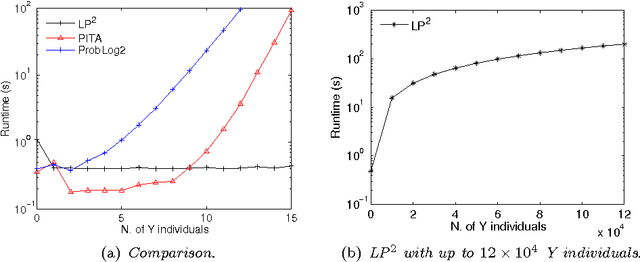
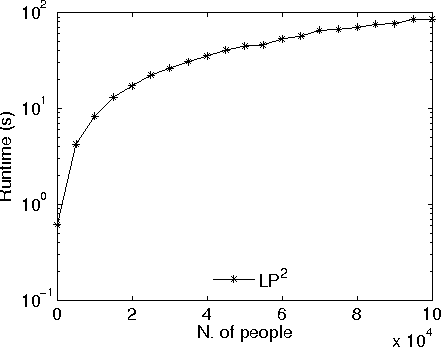
Lifted inference has been proposed for various probabilistic logical frameworks in order to compute the probability of queries in a time that depends on the size of the domains of the random variables rather than the number of instances. Even if various authors have underlined its importance for probabilistic logic programming (PLP), lifted inference has been applied up to now only to relational languages outside of logic programming. In this paper we adapt Generalized Counting First Order Variable Elimination (GC-FOVE) to the problem of computing the probability of queries to probabilistic logic programs under the distribution semantics. In particular, we extend the Prolog Factor Language (PFL) to include two new types of factors that are needed for representing ProbLog programs. These factors take into account the existing causal independence relationships among random variables and are managed by the extension to variable elimination proposed by Zhang and Poole for dealing with convergent variables and heterogeneous factors. Two new operators are added to GC-FOVE for treating heterogeneous factors. The resulting algorithm, called LP$^2$ for Lifted Probabilistic Logic Programming, has been implemented by modifying the PFL implementation of GC-FOVE and tested on three benchmarks for lifted inference. A comparison with PITA and ProbLog2 shows the potential of the approach.

A CHR-based Implementation of Known Arc-Consistency

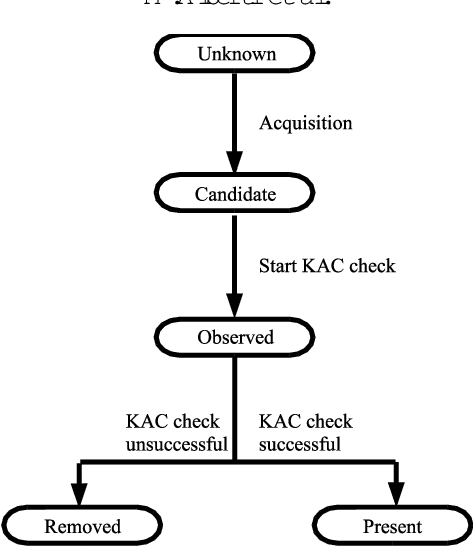
In classical CLP(FD) systems, domains of variables are completely known at the beginning of the constraint propagation process. However, in systems interacting with an external environment, acquiring the whole domains of variables before the beginning of constraint propagation may cause waste of computation time, or even obsolescence of the acquired data at the time of use. For such cases, the Interactive Constraint Satisfaction Problem (ICSP) model has been proposed as an extension of the CSP model, to make it possible to start constraint propagation even when domains are not fully known, performing acquisition of domain elements only when necessary, and without the need for restarting the propagation after every acquisition. In this paper, we show how a solver for the two sorted CLP language, defined in previous work, to express ICSPs, has been implemented in the Constraint Handling Rules (CHR) language, a declarative language particularly suitable for high level implementation of constraint solvers.