Riccardo Rovatti
Multi-Layer Confidence Scoring for Detection of Out-of-Distribution Samples, Adversarial Attacks, and In-Distribution Misclassifications
Dec 22, 2025Abstract:The recent explosive growth in Deep Neural Networks applications raises concerns about the black-box usage of such models, with limited trasparency and trustworthiness in high-stakes domains, which have been crystallized as regulatory requirements such as the European Union Artificial Intelligence Act. While models with embedded confidence metrics have been proposed, such approaches cannot be applied to already existing models without retraining, limiting their broad application. On the other hand, post-hoc methods, which evaluate pre-trained models, focus on solving problems related to improving the confidence in the model's predictions, and detecting Out-Of-Distribution or Adversarial Attacks samples as independent applications. To tackle the limited applicability of already existing methods, we introduce Multi-Layer Analysis for Confidence Scoring (MACS), a unified post-hoc framework that analyzes intermediate activations to produce classification-maps. From the classification-maps, we derive a score applicable for confidence estimation, detecting distributional shifts and adversarial attacks, unifying the three problems in a common framework, and achieving performances that surpass the state-of-the-art approaches in our experiments with the VGG16 and ViTb16 models with a fraction of their computational overhead.
Goal-Oriented Joint Source-Channel Coding: Distortion-Classification-Power Trade-off
Sep 17, 2025
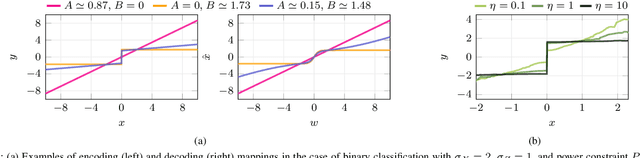
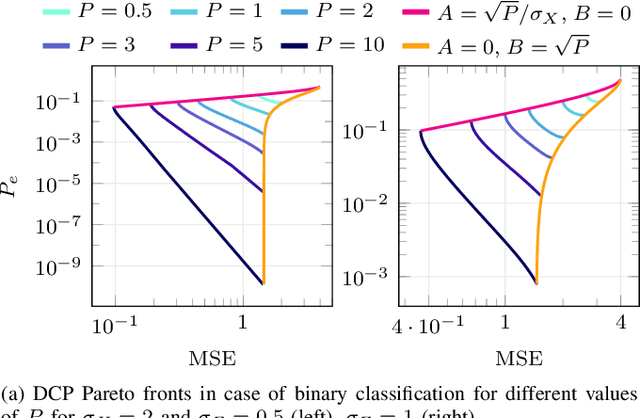
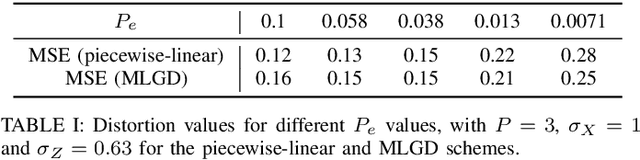
Abstract:Joint source-channel coding is a compelling paradigm when low-latency and low-complexity communication is required. This work proposes a theoretical framework that integrates classification and anomaly detection within the conventional signal reconstruction objective. Assuming a Gaussian scalar source and constraining the encoder to piecewise linear mappings, we derive tractable design rules and explicitly characterize the trade-offs between distortion, classification error, and transmission power.
Legal Summarisation through LLMs: The PRODIGIT Project
Aug 04, 2023


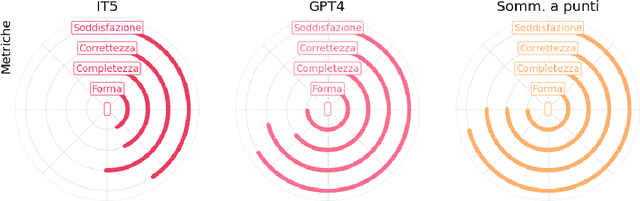
Abstract:We present some initial results of a large-scale Italian project called PRODIGIT which aims to support tax judges and lawyers through digital technology, focusing on AI. We have focused on generation of summaries of judicial decisions and on the extraction of related information, such as the identification of legal issues and decision-making criteria, and the specification of keywords. To this end, we have deployed and evaluated different tools and approaches to extractive and abstractive summarisation. We have applied LLMs, and particularly on GPT4, which has enabled us to obtain results that proved satisfactory, according to an evaluation by expert tax judges and lawyers. On this basis, a prototype application is being built which will be made publicly available.
Anomaly Detection based on Compressed Data: an Information Theoretic Characterization
Oct 06, 2021
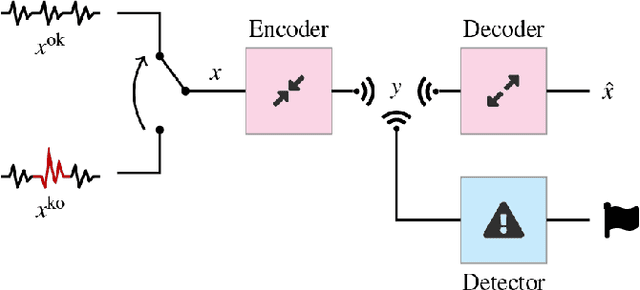


Abstract:We analyze the effect of lossy compression in the processing of sensor signals that must be used to detect anomalous events in the system under observation. The intuitive relationship between the quality loss at higher compression and the possibility of telling anomalous behaviours from normal ones is formalized in terms of information-theoretic quantities. Some analytic derivations are made within the Gaussian framework and possibly in the asymptotic regime for what concerns the stretch of signals considered. Analytical conclusions are matched with the performance of practical detectors in a toy case allowing the assessment of different compression/detector configurations.
Rakeness in the design of Analog-to-Information Conversion of Sparse and Localized Signals
May 05, 2012



Abstract:Design of Random Modulation Pre-Integration systems based on the restricted-isometry property may be suboptimal when the energy of the signals to be acquired is not evenly distributed, i.e. when they are both sparse and localized. To counter this, we introduce an additional design criterion, that we call rakeness, accounting for the amount of energy that the measurements capture from the signal to be acquired. Hence, for localized signals a proper system tuning increases the rakeness as well as the average SNR of the samples used in its reconstruction. Yet, maximizing average SNR may go against the need of capturing all the components that are potentially non-zero in a sparse signal, i.e., against the restricted isometry requirement ensuring reconstructability. What we propose is to administer the trade-off between rakeness and restricted isometry in a statistical way by laying down an optimization problem. The solution of such an optimization problem is the statistic of the process generating the random waveforms onto which the signal is projected to obtain the measurements. The formal definition of such a problems is given as well as its solution for signals that are either localized in frequency or in more generic domain. Sample applications, to ECG signals and small images of printed letters and numbers, show that rakeness-based design leads to non-negligible improvements in both cases.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge