Reza Namazi
SMGRL: A Scalable Multi-resolution Graph Representation Learning Framework
Jan 29, 2022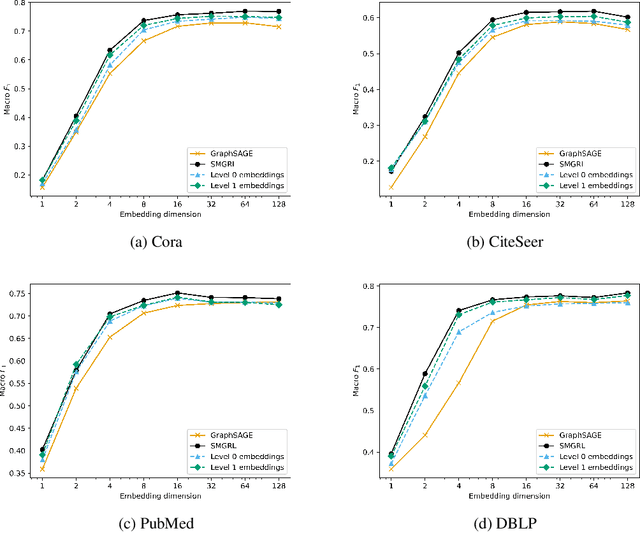
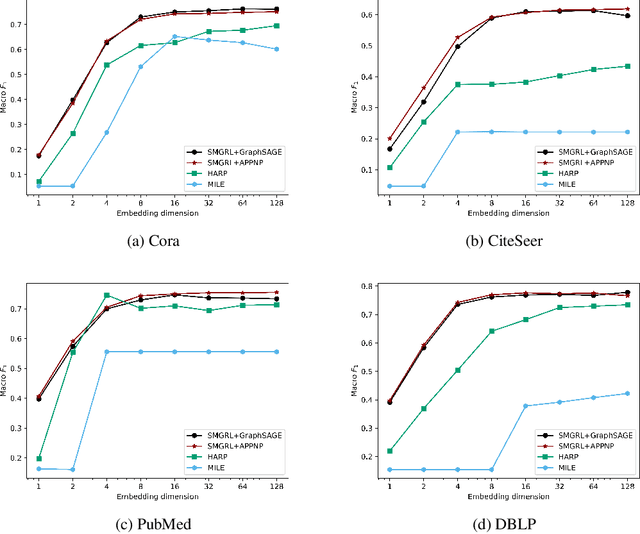
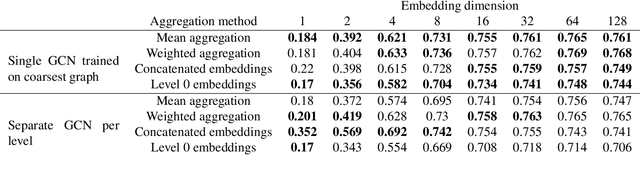
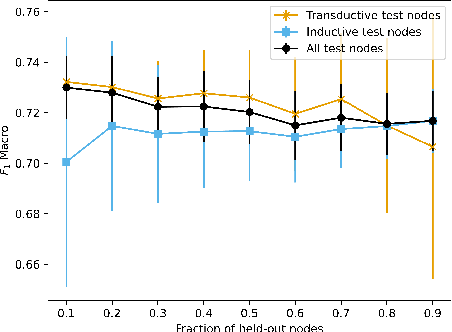
Abstract:Graph convolutional networks (GCNs) allow us to learn topologically-aware node embeddings, which can be useful for classification or link prediction. However, by construction, they lack positional awareness and are unable to capture long-range dependencies without adding additional layers -- which in turn leads to over-smoothing and increased time and space complexity. Further, the complex dependencies between nodes make mini-batching challenging, limiting their applicability to large graphs. This paper proposes a Scalable Multi-resolution Graph Representation Learning (SMGRL) framework that enables us to learn multi-resolution node embeddings efficiently. Our framework is model-agnostic and can be applied to any existing GCN model. We dramatically reduce training costs by training only on a reduced-dimension coarsening of the original graph, then exploit self-similarity to apply the resulting algorithm at multiple resolutions. Inference of these multi-resolution embeddings can be distributed across multiple machines to reduce computational and memory requirements further. The resulting multi-resolution embeddings can be aggregated to yield high-quality node embeddings that capture both long- and short-range dependencies between nodes. Our experiments show that this leads to improved classification accuracy, without incurring high computational costs.
GL-Coarsener: A Graph representation learning framework to construct coarse grid hierarchy for AMG solvers
Nov 19, 2020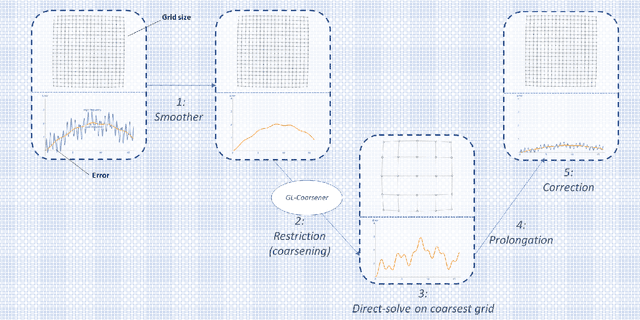
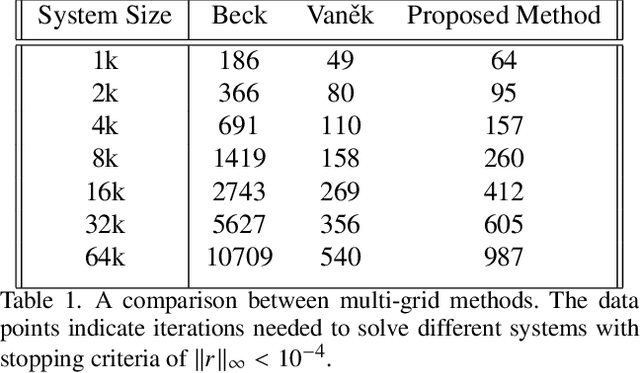
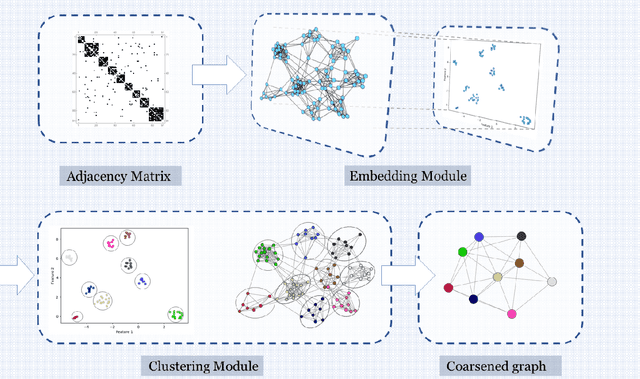
Abstract:In many numerical schemes, the computational complexity scales non-linearly with the problem size. Solving a linear system of equations using direct methods or most iterative methods is a typical example. Algebraic multi-grid (AMG) methods are numerical methods used to solve large linear systems of equations efficiently. One of the main differences between AMG methods is how the coarser grid is constructed from a given fine grid. There are two main classes of AMG methods; graph and aggregation based coarsening methods. Here we propose an aggregation-based coarsening framework leveraging graph representation learning and clustering algorithms. Our method introduces the power of machine learning into the AMG research field and opens a new perspective for future researches. The proposed method uses graph representation learning techniques to learn latent features of the graph obtained from the underlying matrix of coefficients. Using these extracted features, we generated a coarser grid from the fine grid. The proposed method is highly capable of parallel computations. Our experiments show that the proposed method's efficiency in solving large systems is closely comparable with other aggregation-based methods, demonstrating the high capability of graph representation learning in designing multi-grid solvers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge