Compassionately Conservative Balanced Cuts for Image Segmentation

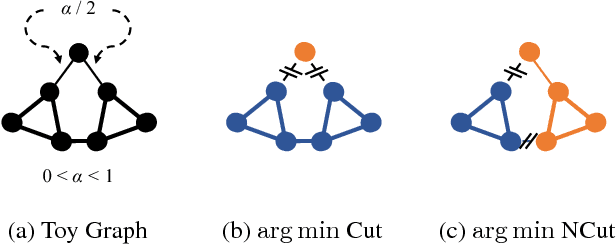
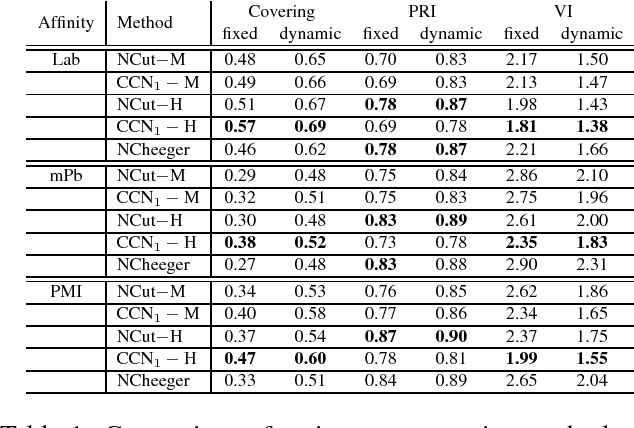
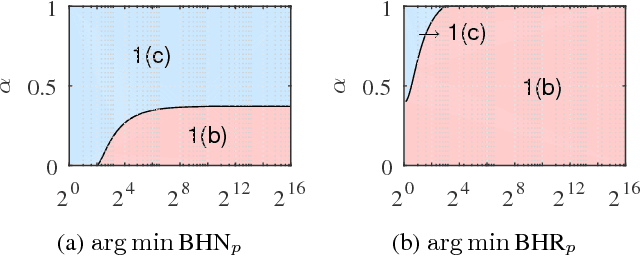
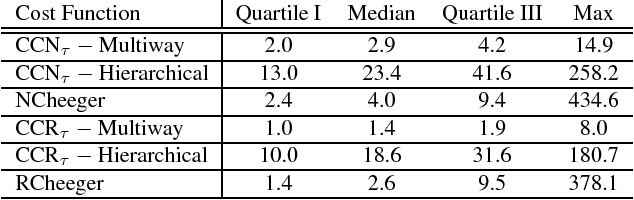
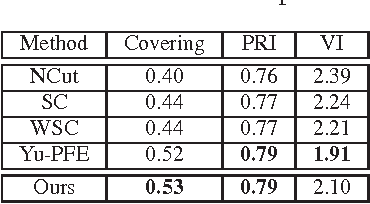
The Normalized Cut (NCut) objective function, widely used in data clustering and image segmentation, quantifies the cost of graph partitioning in a way that biases clusters or segments that are balanced towards having lower values than unbalanced partitionings. However, this bias is so strong that it avoids any singleton partitions, even when vertices are very weakly connected to the rest of the graph. Motivated by the B\"uhler-Hein family of balanced cut costs, we propose the family of Compassionately Conservative Balanced (CCB) Cut costs, which are indexed by a parameter that can be used to strike a compromise between the desire to avoid too many singleton partitions and the notion that all partitions should be balanced. We show that CCB-Cut minimization can be relaxed into an orthogonally constrained $\ell_{\tau}$-minimization problem that coincides with the problem of computing Piecewise Flat Embeddings (PFE) for one particular index value, and we present an algorithm for solving the relaxed problem by iteratively minimizing a sequence of reweighted Rayleigh quotients (IRRQ). Using images from the BSDS500 database, we show that image segmentation based on CCB-Cut minimization provides better accuracy with respect to ground truth and greater variability in region size than NCut-based image segmentation.

Efficiently Computing Piecewise Flat Embeddings for Data Clustering and Image Segmentation

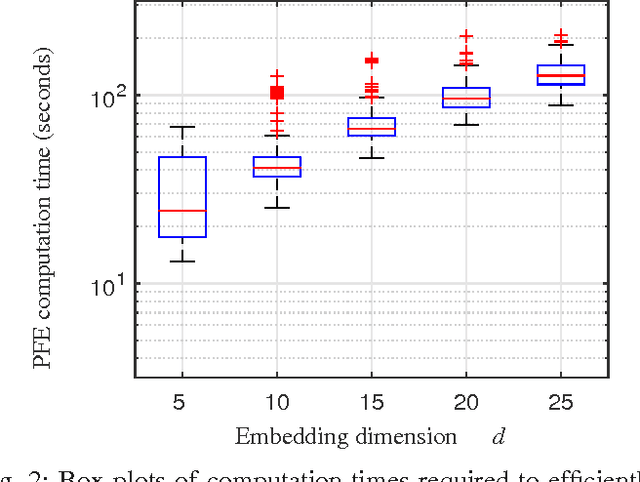
Image segmentation is a popular area of research in computer vision that has many applications in automated image processing. A recent technique called piecewise flat embeddings (PFE) has been proposed for use in image segmentation; PFE transforms image pixel data into a lower dimensional representation where similar pixels are pulled close together and dissimilar pixels are pushed apart. This technique has shown promising results, but its original formulation is not computationally feasible for large images. We propose two improvements to the algorithm for computing PFE: first, we reformulate portions of the algorithm to enable various linear algebra operations to be performed in parallel; second, we propose utilizing an iterative linear solver (preconditioned conjugate gradient) to quickly solve a linear least-squares problem that occurs in the inner loop of a nested iteration. With these two computational improvements, we show on a publicly available image database that PFE can be sped up by an order of magnitude without sacrificing segmentation performance. Our results make this technique more practical for use on large data sets, not only for image segmentation, but for general data clustering problems.