John F. Hamilton
Compassionately Conservative Balanced Cuts for Image Segmentation
Mar 27, 2018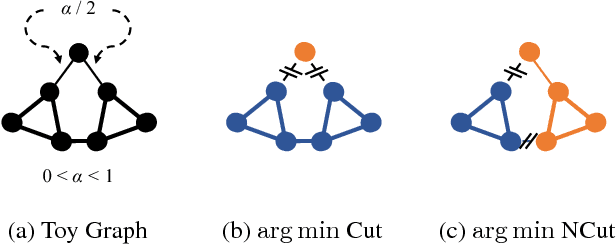
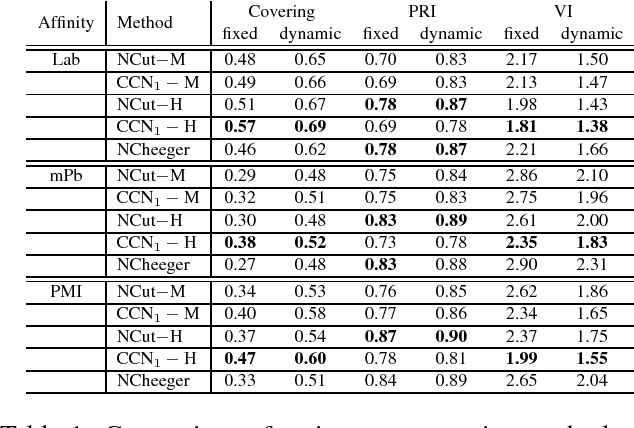
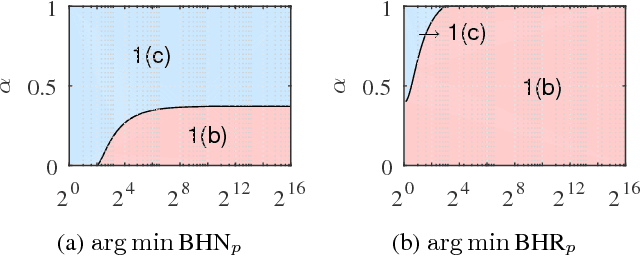
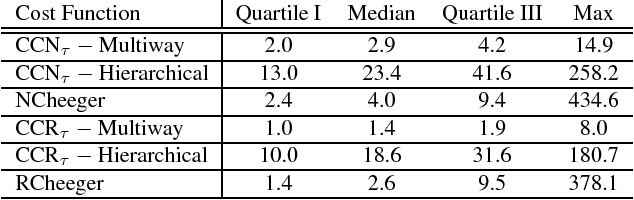
Abstract:The Normalized Cut (NCut) objective function, widely used in data clustering and image segmentation, quantifies the cost of graph partitioning in a way that biases clusters or segments that are balanced towards having lower values than unbalanced partitionings. However, this bias is so strong that it avoids any singleton partitions, even when vertices are very weakly connected to the rest of the graph. Motivated by the B\"uhler-Hein family of balanced cut costs, we propose the family of Compassionately Conservative Balanced (CCB) Cut costs, which are indexed by a parameter that can be used to strike a compromise between the desire to avoid too many singleton partitions and the notion that all partitions should be balanced. We show that CCB-Cut minimization can be relaxed into an orthogonally constrained $\ell_{\tau}$-minimization problem that coincides with the problem of computing Piecewise Flat Embeddings (PFE) for one particular index value, and we present an algorithm for solving the relaxed problem by iteratively minimizing a sequence of reweighted Rayleigh quotients (IRRQ). Using images from the BSDS500 database, we show that image segmentation based on CCB-Cut minimization provides better accuracy with respect to ground truth and greater variability in region size than NCut-based image segmentation.
Multiple-View Spectral Clustering for Group-wise Functional Community Detection
Nov 21, 2016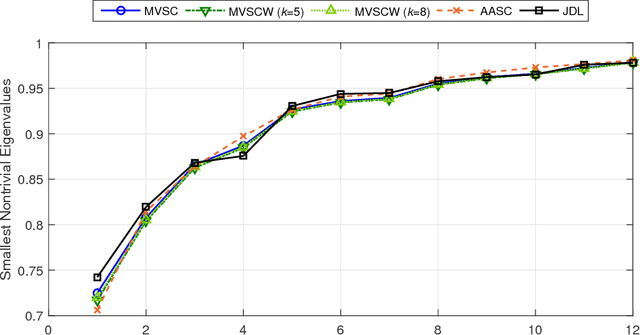
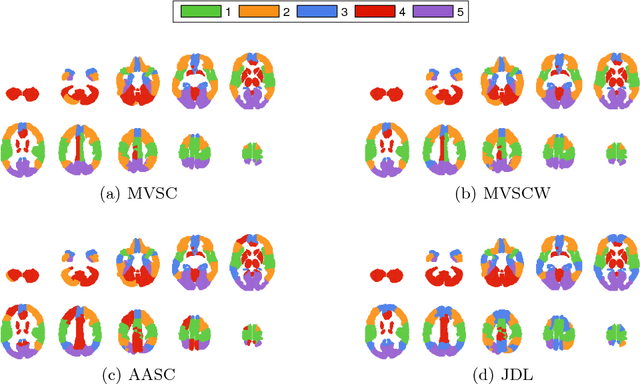
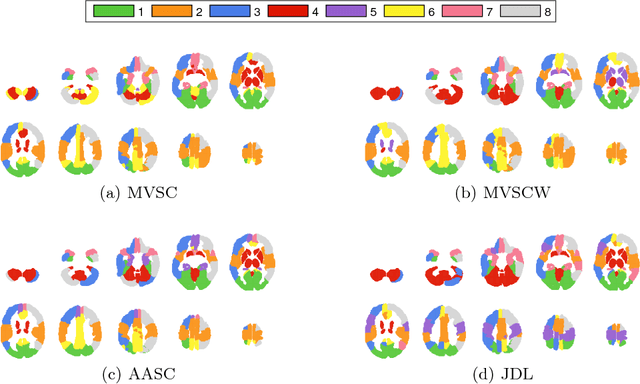
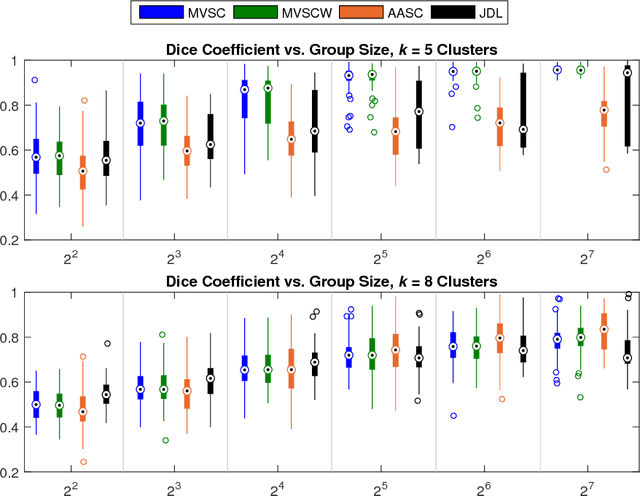
Abstract:Functional connectivity analysis yields powerful insights into our understanding of the human brain. Group-wise functional community detection aims to partition the brain into clusters, or communities, in which functional activity is inter-regionally correlated in a common manner across a group of subjects. In this article, we show how to use multiple-view spectral clustering to perform group-wise functional community detection. In a series of experiments on 291 subjects from the Human Connectome Project, we compare three versions of multiple-view spectral clustering: MVSC (uniform weights), MVSCW (weights based on subject-specific embedding quality), and AASC (weights optimized along with the embedding) with the competing technique of Joint Diagonalization of Laplacians (JDL). Results show that multiple-view spectral clustering not only yields group-wise functional communities that are more consistent than JDL when using randomly selected subsets of individual brains, but it is several orders of magnitude faster than JDL.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge