Efficiently Computing Piecewise Flat Embeddings for Data Clustering and Image Segmentation
Paper and Code
Dec 20, 2016
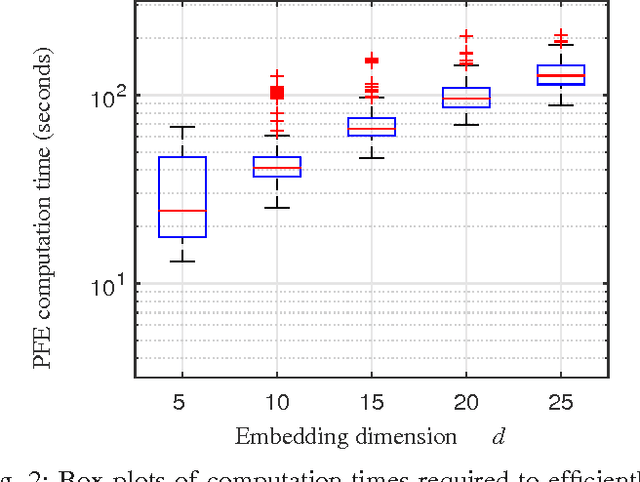
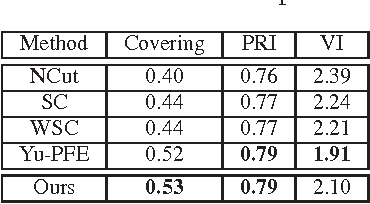
Image segmentation is a popular area of research in computer vision that has many applications in automated image processing. A recent technique called piecewise flat embeddings (PFE) has been proposed for use in image segmentation; PFE transforms image pixel data into a lower dimensional representation where similar pixels are pulled close together and dissimilar pixels are pushed apart. This technique has shown promising results, but its original formulation is not computationally feasible for large images. We propose two improvements to the algorithm for computing PFE: first, we reformulate portions of the algorithm to enable various linear algebra operations to be performed in parallel; second, we propose utilizing an iterative linear solver (preconditioned conjugate gradient) to quickly solve a linear least-squares problem that occurs in the inner loop of a nested iteration. With these two computational improvements, we show on a publicly available image database that PFE can be sped up by an order of magnitude without sacrificing segmentation performance. Our results make this technique more practical for use on large data sets, not only for image segmentation, but for general data clustering problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge