Triformer: Triangular, Variable-Specific Attentions for Long Sequence Multivariate Time Series Forecasting--Full Version

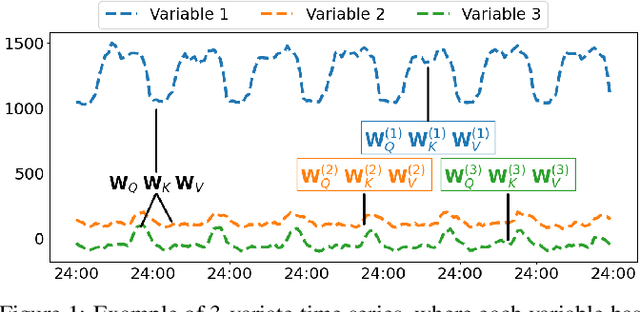
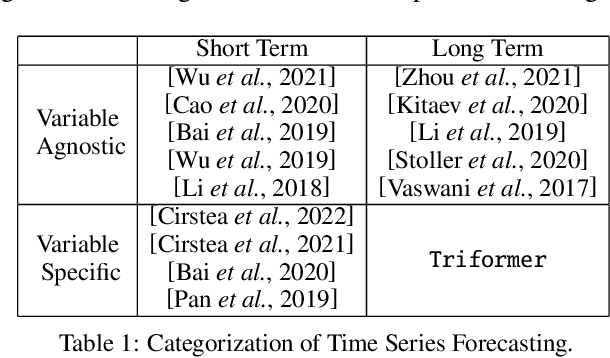
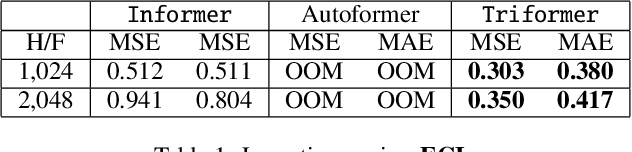
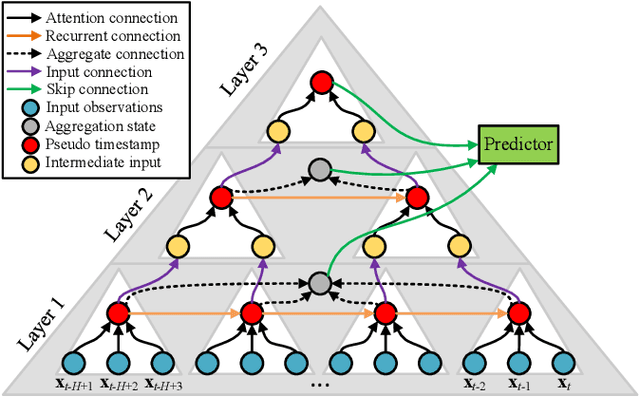
A variety of real-world applications rely on far future information to make decisions, thus calling for efficient and accurate long sequence multivariate time series forecasting. While recent attention-based forecasting models show strong abilities in capturing long-term dependencies, they still suffer from two key limitations. First, canonical self attention has a quadratic complexity w.r.t. the input time series length, thus falling short in efficiency. Second, different variables' time series often have distinct temporal dynamics, which existing studies fail to capture, as they use the same model parameter space, e.g., projection matrices, for all variables' time series, thus falling short in accuracy. To ensure high efficiency and accuracy, we propose Triformer, a triangular, variable-specific attention. (i) Linear complexity: we introduce a novel patch attention with linear complexity. When stacking multiple layers of the patch attentions, a triangular structure is proposed such that the layer sizes shrink exponentially, thus maintaining linear complexity. (ii) Variable-specific parameters: we propose a light-weight method to enable distinct sets of model parameters for different variables' time series to enhance accuracy without compromising efficiency and memory usage. Strong empirical evidence on four datasets from multiple domains justifies our design choices, and it demonstrates that Triformer outperforms state-of-the-art methods w.r.t. both accuracy and efficiency. This is an extended version of "Triformer: Triangular, Variable-Specific Attentions for Long Sequence Multivariate Time Series Forecasting", to appear in IJCAI 2022 [Cirstea et al., 2022a], including additional experimental results.

Towards Spatio-Temporal Aware Traffic Time Series Forecasting--Full Version

Traffic time series forecasting is challenging due to complex spatio-temporal dynamics time series from different locations often have distinct patterns; and for the same time series, patterns may vary across time, where, for example, there exist certain periods across a day showing stronger temporal correlations. Although recent forecasting models, in particular deep learning based models, show promising results, they suffer from being spatio-temporal agnostic. Such spatio-temporal agnostic models employ a shared parameter space irrespective of the time series locations and the time periods and they assume that the temporal patterns are similar across locations and do not evolve across time, which may not always hold, thus leading to sub-optimal results. In this work, we propose a framework that aims at turning spatio-temporal agnostic models to spatio-temporal aware models. To do so, we encode time series from different locations into stochastic variables, from which we generate location-specific and time-varying model parameters to better capture the spatio-temporal dynamics. We show how to integrate the framework with canonical attentions to enable spatio-temporal aware attentions. Next, to compensate for the additional overhead introduced by the spatio-temporal aware model parameter generation process, we propose a novel window attention scheme, which helps reduce the complexity from quadratic to linear, making spatio-temporal aware attentions also have competitive efficiency. We show strong empirical evidence on four traffic time series datasets, where the proposed spatio-temporal aware attentions outperform state-of-the-art methods in term of accuracy and efficiency. This is an extended version of "Towards Spatio-Temporal Aware Traffic Time Series Forecasting", to appear in ICDE 2022 [1], including additional experimental results.

Graph Attention Recurrent Neural Networks for Correlated Time Series Forecasting -- Full version

We consider a setting where multiple entities inter-act with each other over time and the time-varying statuses of the entities are represented as multiple correlated time series. For example, speed sensors are deployed in different locations in a road network, where the speed of a specific location across time is captured by the corresponding sensor as a time series, resulting in multiple speed time series from different locations, which are often correlated. To enable accurate forecasting on correlated time series, we proposes graph attention recurrent neural networks.First, we build a graph among different entities by taking into account spatial proximity and employ a multi-head attention mechanism to derive adaptive weight matrices for the graph to capture the correlations among vertices (e.g., speeds at different locations) at different timestamps. Second, we employ recurrent neural networks to take into account temporal dependency while taking into account the adaptive weight matrices learned from the first step to consider the correlations among time series.Experiments on a large real-world speed time series data set suggest that the proposed method is effective and outperforms the state-of-the-art in most settings. This manuscript provides a full version of a workshop paper [1].

Correlated Time Series Forecasting using Deep Neural Networks: A Summary of Results

Cyber-physical systems often consist of entities that interact with each other over time. Meanwhile, as part of the continued digitization of industrial processes, various sensor technologies are deployed that enable us to record time-varying attributes (a.k.a., time series) of such entities, thus producing correlated time series. To enable accurate forecasting on such correlated time series, this paper proposes two models that combine convolutional neural networks (CNNs) and recurrent neural networks (RNNs). The first model employs a CNN on each individual time series, combines the convoluted features, and then applies an RNN on top of the convoluted features in the end to enable forecasting. The second model adds additional auto-encoders into the individual CNNs, making the second model a multi-task learning model, which provides accurate and robust forecasting. Experiments on two real-world correlated time series data set suggest that the proposed two models are effective and outperform baselines in most settings. This report extends the paper "Correlated Time Series Forecasting using Multi-Task Deep Neural Networks," to appear in ACM CIKM 2018, by providing additional experimental results.