On the Definiteness of Earth Mover's Distance and Its Relation to Set Intersection

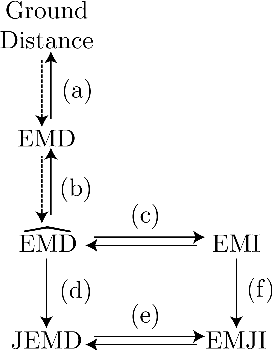
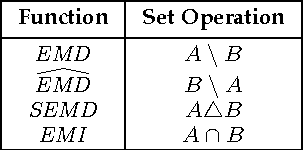
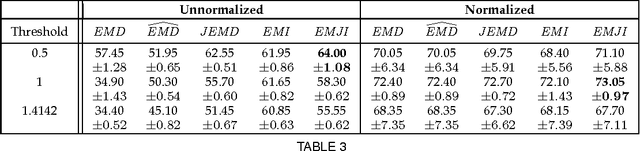
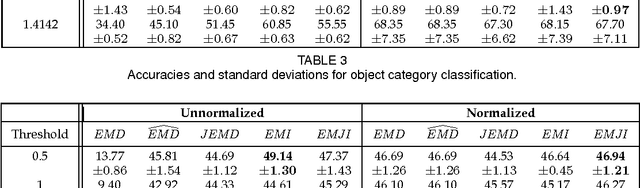
Positive definite kernels are an important tool in machine learning that enable efficient solutions to otherwise difficult or intractable problems by implicitly linearizing the problem geometry. In this paper we develop a set-theoretic interpretation of the Earth Mover's Distance (EMD) and propose Earth Mover's Intersection (EMI), a positive definite analog to EMD for sets of different sizes. We provide conditions under which EMD or certain approximations to EMD are negative definite. We also present a positive-definite-preserving transformation that can be applied to any kernel and can also be used to derive positive definite EMD-based kernels and show that the Jaccard index is simply the result of this transformation. Finally, we evaluate kernels based on EMI and the proposed transformation versus EMD in various computer vision tasks and show that EMD is generally inferior even with indefinite kernel techniques.

Classifying Unordered Feature Sets with Convolutional Deep Averaging Networks

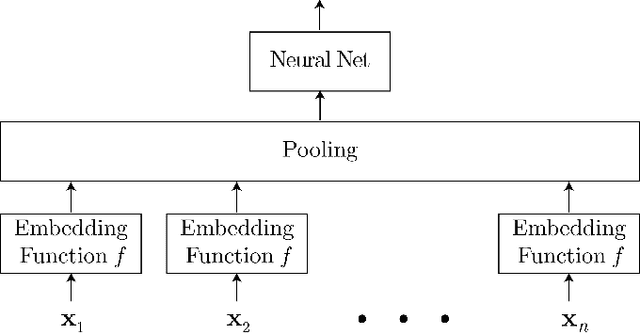
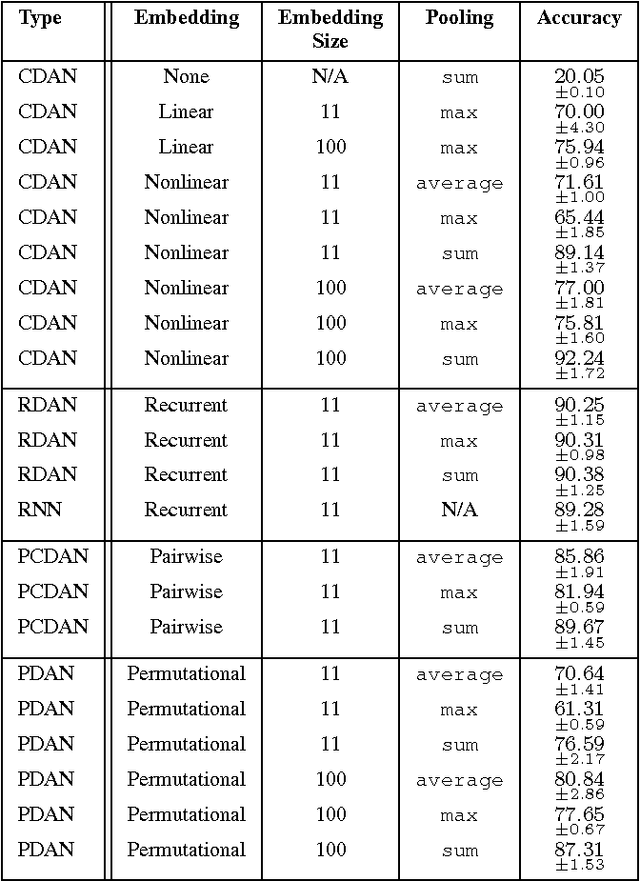
Unordered feature sets are a nonstandard data structure that traditional neural networks are incapable of addressing in a principled manner. Providing a concatenation of features in an arbitrary order may lead to the learning of spurious patterns or biases that do not actually exist. Another complication is introduced if the number of features varies between each set. We propose convolutional deep averaging networks (CDANs) for classifying and learning representations of datasets whose instances comprise variable-size, unordered feature sets. CDANs are efficient, permutation-invariant, and capable of accepting sets of arbitrary size. We emphasize the importance of nonlinear feature embeddings for obtaining effective CDAN classifiers and illustrate their advantages in experiments versus linear embeddings and alternative permutation-invariant and -equivariant architectures.