On the Definiteness of Earth Mover's Distance and Its Relation to Set Intersection
Paper and Code
Aug 21, 2018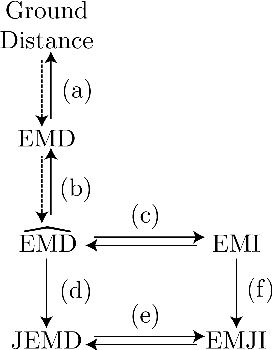
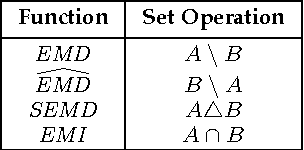
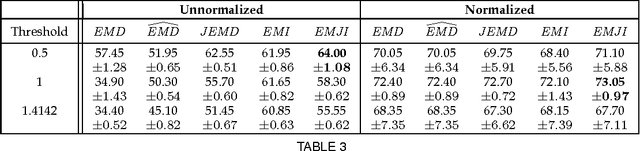
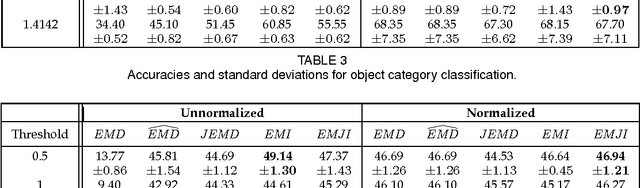
Positive definite kernels are an important tool in machine learning that enable efficient solutions to otherwise difficult or intractable problems by implicitly linearizing the problem geometry. In this paper we develop a set-theoretic interpretation of the Earth Mover's Distance (EMD) and propose Earth Mover's Intersection (EMI), a positive definite analog to EMD for sets of different sizes. We provide conditions under which EMD or certain approximations to EMD are negative definite. We also present a positive-definite-preserving transformation that can be applied to any kernel and can also be used to derive positive definite EMD-based kernels and show that the Jaccard index is simply the result of this transformation. Finally, we evaluate kernels based on EMI and the proposed transformation versus EMD in various computer vision tasks and show that EMD is generally inferior even with indefinite kernel techniques.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge