Classifying Unordered Feature Sets with Convolutional Deep Averaging Networks
Paper and Code
Sep 10, 2017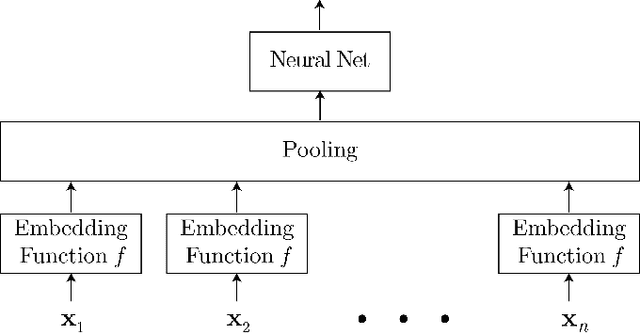
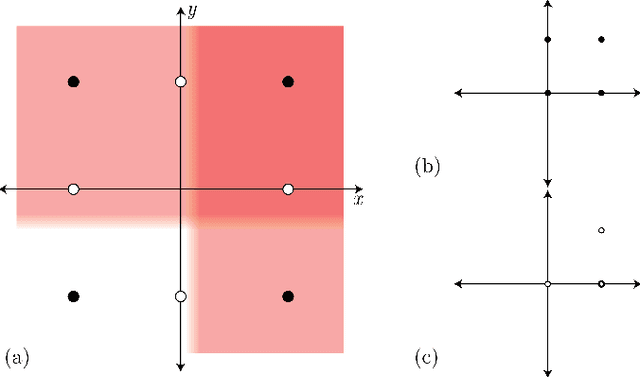
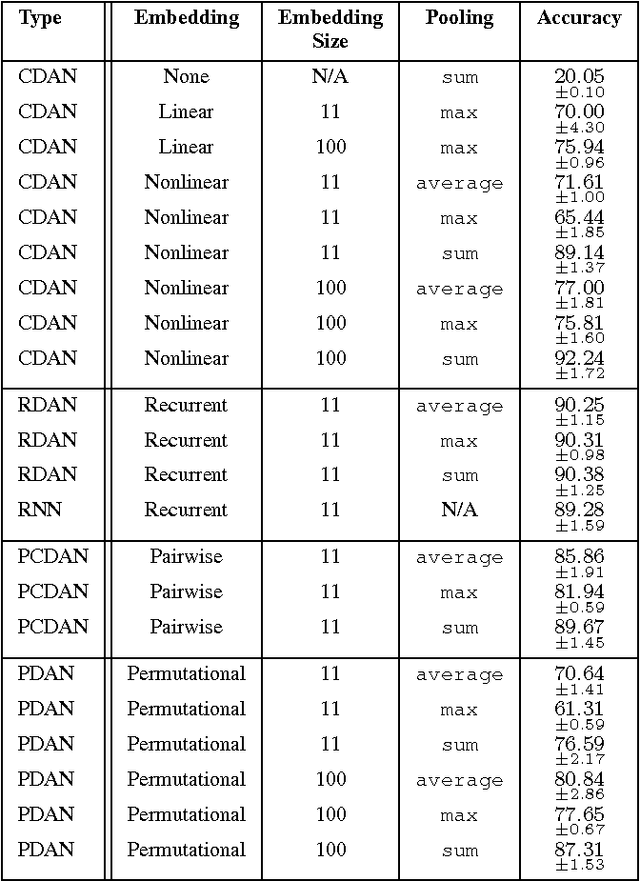
Unordered feature sets are a nonstandard data structure that traditional neural networks are incapable of addressing in a principled manner. Providing a concatenation of features in an arbitrary order may lead to the learning of spurious patterns or biases that do not actually exist. Another complication is introduced if the number of features varies between each set. We propose convolutional deep averaging networks (CDANs) for classifying and learning representations of datasets whose instances comprise variable-size, unordered feature sets. CDANs are efficient, permutation-invariant, and capable of accepting sets of arbitrary size. We emphasize the importance of nonlinear feature embeddings for obtaining effective CDAN classifiers and illustrate their advantages in experiments versus linear embeddings and alternative permutation-invariant and -equivariant architectures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge