Tree-based Subgroup Discovery In Electronic Health Records: Heterogeneity of Treatment Effects for DTG-containing Therapies

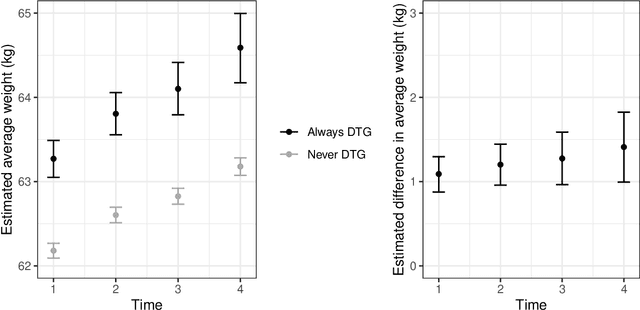
The rich longitudinal individual level data available from electronic health records (EHRs) can be used to examine treatment effect heterogeneity. However, estimating treatment effects using EHR data poses several challenges, including time-varying confounding, repeated and temporally non-aligned measurements of covariates, treatment assignments and outcomes, and loss-to-follow-up due to dropout. Here, we develop the Subgroup Discovery for Longitudinal Data (SDLD) algorithm, a tree-based algorithm for discovering subgroups with heterogeneous treatment effects using longitudinal data by combining the generalized interaction tree algorithm, a general data-driven method for subgroup discovery, with longitudinal targeted maximum likelihood estimation. We apply the algorithm to EHR data to discover subgroups of people living with human immunodeficiency virus (HIV) who are at higher risk of weight gain when receiving dolutegravir-containing antiretroviral therapies (ARTs) versus when receiving non dolutegravir-containing ARTs.

Inference for BART with Multinomial Outcomes

The multinomial probit Bayesian additive regression trees (MPBART) framework was proposed by Kindo et al. (KD), approximating the latent utilities in the multinomial probit (MNP) model with BART (Chipman et al. 2010). Compared to multinomial logistic models, MNP does not assume independent alternatives and the correlation structure among alternatives can be specified through multivariate Gaussian distributed latent utilities. We introduce two new algorithms for fitting the MPBART and show that the theoretical mixing rates of our proposals are equal or superior to the existing algorithm in KD. Through simulations, we explore the robustness of the methods to the choice of reference level, imbalance in outcome frequencies, and the specifications of prior hyperparameters for the utility error term. The work is motivated by the application of generating posterior predictive distributions for mortality and engagement in care among HIV-positive patients based on electronic health records (EHRs) from the Academic Model Providing Access to Healthcare (AMPATH) in Kenya. In both the application and simulations, we observe better performance using our proposals as compared to KD in terms of MCMC convergence rate and posterior predictive accuracy.

Classification using Ensemble Learning under Weighted Misclassification Loss

Binary classification rules based on covariates typically depend on simple loss functions such as zero-one misclassification. Some cases may require more complex loss functions. For example, individual-level monitoring of HIV-infected individuals on antiretroviral therapy (ART) requires periodic assessment of treatment failure, defined as having a viral load (VL) value above a certain threshold. In some resource limited settings, VL tests may be limited by cost or technology, and diagnoses are based on other clinical markers. Depending on scenario, higher premium may be placed on avoiding false-positives which brings greater cost and reduced treatment options. Here, the optimal rule is determined by minimizing a weighted misclassification loss/risk. We propose a method for finding and cross-validating optimal binary classification rules under weighted misclassification loss. We focus on rules comprising a prediction score and an associated threshold, where the score is derived using an ensemble learner. Simulations and examples show that our method, which derives the score and threshold jointly, more accurately estimates overall risk and has better operating characteristics compared with methods that derive the score first and the cutoff conditionally on the score especially for finite samples.