Theoretical Analysis of the Radio Map Estimation Problem

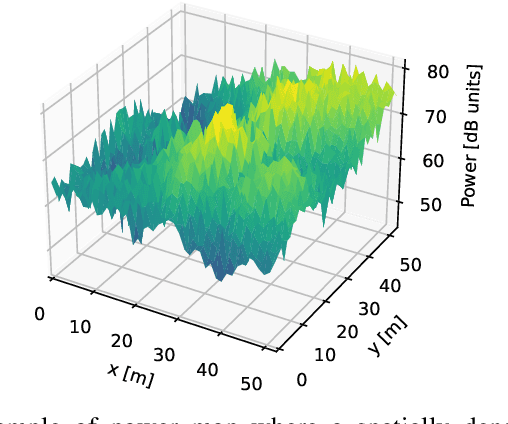
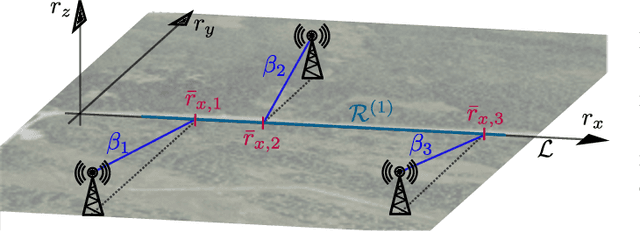
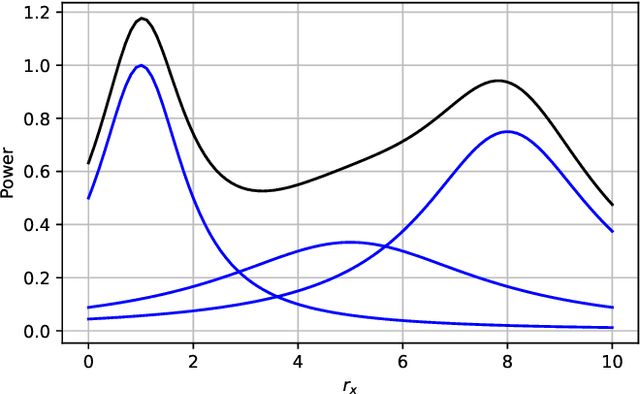
Radio map estimation (RME) constructs representations providing radio frequency metrics, such as the received signal strength, at every location of a geographic area using a set of measurements collected at multiple positions. The resulting radio maps find a wide range of applications in wireless communications, including prediction of coverage holes, network planning, resource allocation, and path planning for mobile robots. Although a vast number of estimators have been proposed, the theoretical understanding of the RME problem has not been pursued. The present work aims at filling this gap along two directions. First, the complexity of the function space of radio maps is quantified by means of lower and upper bounds on their spatial variability, which offers valuable insight into the required spatial distribution of measurements and estimators that can be used. Second, the reconstruction error for power maps in free space is upper bounded for three simple spatial interpolators, namely zeroth-order, first-order, and sinc interpolators. In view of these bounds, the proximity coefficient, which is an increasing function of the transmitted power and a decreasing function of the distance from the transmitters to the mapped region, is proposed to quantify the complexity of the RME problem. Simple numerical experiments assess the tightness of the obtained bounds and reveal the practical trade-offs associated with the considered interpolators.

Radio Map Estimation in the Real-World: Empirical Validation and Analysis

Radio maps quantify received signal strength or other magnitudes of the radio frequency environment at every point of a geographical region. These maps play a vital role in a large number of applications such as wireless network planning, spectrum management, and optimization of communication systems. However, empirical validation of the large number of existing radio map estimators is highly limited. To fill this gap, a large data set of measurements has been collected with an autonomous unmanned aerial vehicle (UAV) and a representative subset of these estimators were evaluated on this data. The performance-complexity trade-off and the impact of fast fading are extensively investigated. Although sophisticated estimators based on deep neural networks (DNNs) exhibit the best performance, they are seen to require large volumes of training data to offer a substantial advantage relative to more traditional schemes. A novel algorithm that blends both kinds of estimators is seen to enjoy the benefits of both, thereby suggesting the potential of exploring this research direction further.

Spectrum Surveying: Active Radio Map Estimation with Autonomous UAVs

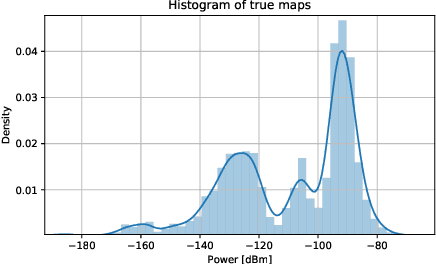
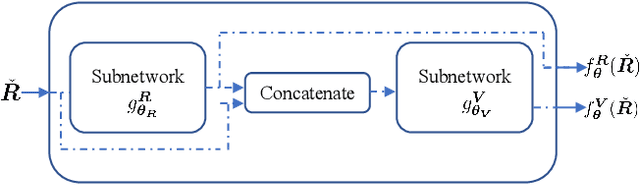
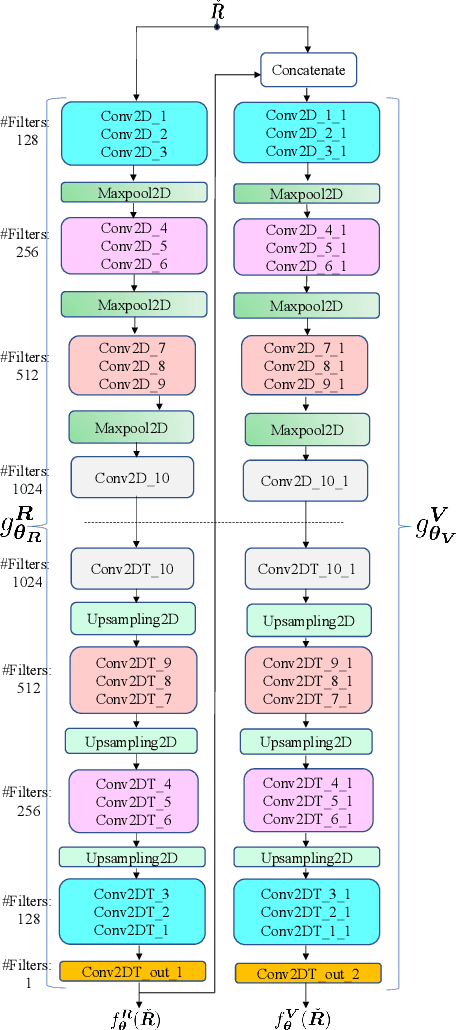
Radio maps find numerous applications in wireless communications and mobile robotics tasks, including resource allocation, interference coordination, and mission planning. Although numerous techniques have been proposed to construct radio maps from spatially distributed measurements, the locations of such measurements are assumed predetermined beforehand. In contrast, this paper proposes spectrum surveying, where a mobile robot such as an unmanned aerial vehicle (UAV) collects measurements at a set of locations that are actively selected to obtain high-quality map estimates in a short surveying time. This is performed in two steps. First, two novel algorithms, a model-based online Bayesian estimator and a data-driven deep learning algorithm, are devised for updating a map estimate and an uncertainty metric that indicates the informativeness of measurements at each possible location. These algorithms offer complementary benefits and feature constant complexity per measurement. Second, the uncertainty metric is used to plan the trajectory of the UAV to gather measurements at the most informative locations. To overcome the combinatorial complexity of this problem, a dynamic programming approach is proposed to obtain lists of waypoints through areas of large uncertainty in linear time. Numerical experiments conducted on a realistic dataset confirm that the proposed scheme constructs accurate radio maps quickly.