Theoretical Analysis of the Radio Map Estimation Problem

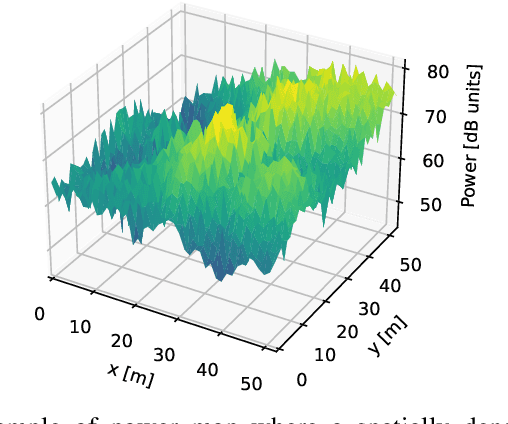
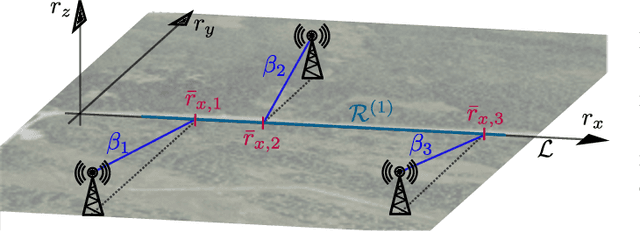
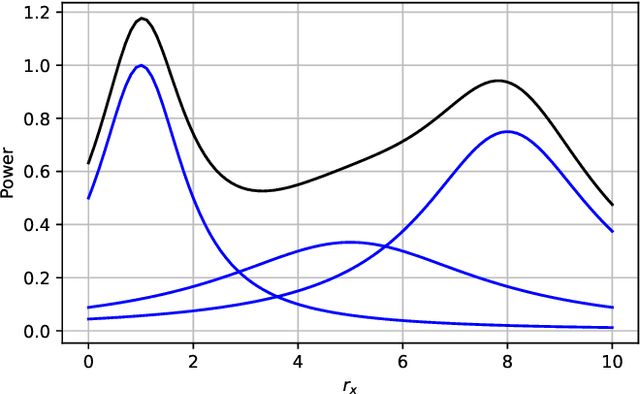
Radio map estimation (RME) constructs representations providing radio frequency metrics, such as the received signal strength, at every location of a geographic area using a set of measurements collected at multiple positions. The resulting radio maps find a wide range of applications in wireless communications, including prediction of coverage holes, network planning, resource allocation, and path planning for mobile robots. Although a vast number of estimators have been proposed, the theoretical understanding of the RME problem has not been pursued. The present work aims at filling this gap along two directions. First, the complexity of the function space of radio maps is quantified by means of lower and upper bounds on their spatial variability, which offers valuable insight into the required spatial distribution of measurements and estimators that can be used. Second, the reconstruction error for power maps in free space is upper bounded for three simple spatial interpolators, namely zeroth-order, first-order, and sinc interpolators. In view of these bounds, the proximity coefficient, which is an increasing function of the transmitted power and a decreasing function of the distance from the transmitters to the mapped region, is proposed to quantify the complexity of the RME problem. Simple numerical experiments assess the tightness of the obtained bounds and reveal the practical trade-offs associated with the considered interpolators.