Adversarial Vulnerability as a Consequence of On-Manifold Inseparibility

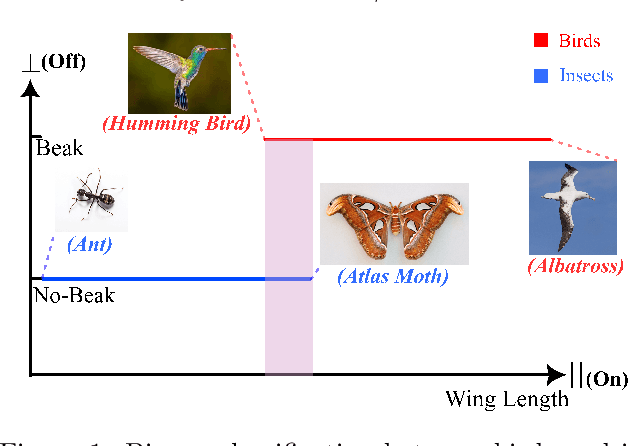
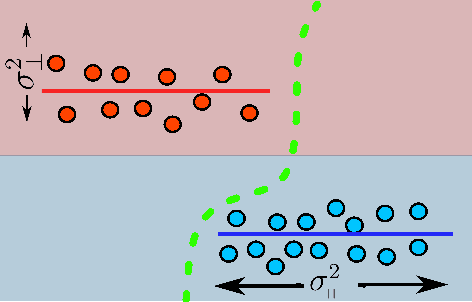
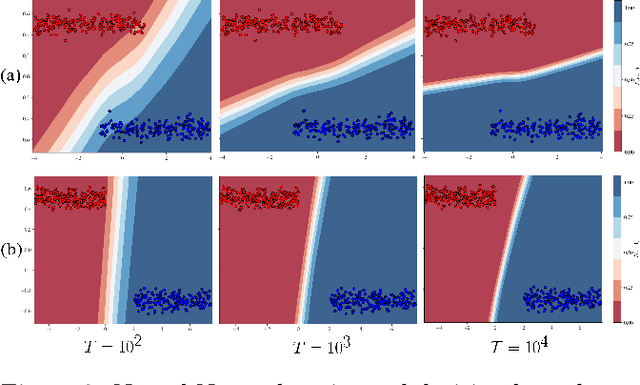
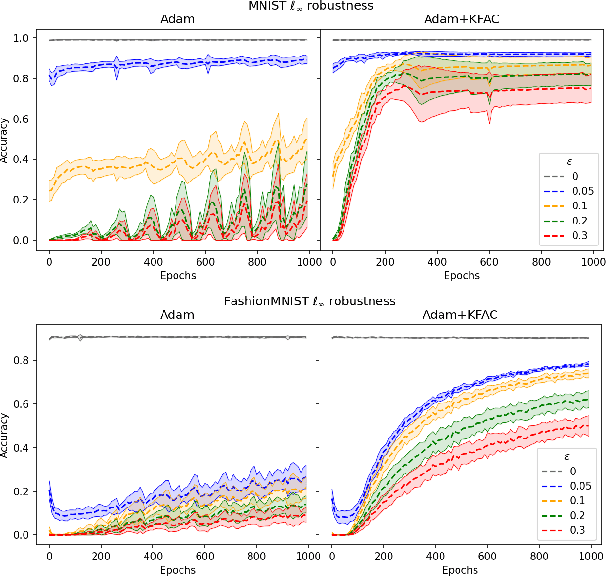
Recent works have shown theoretically and empirically that redundant data dimensions are a source of adversarial vulnerability. However, the inverse doesn't seem to hold in practice; employing dimension-reduction techniques doesn't exhibit robustness as expected. In this work, we consider classification tasks and characterize the data distribution as a low-dimensional manifold, with high/low variance features defining the on/off manifold direction. We argue that clean training experiences poor convergence in the off-manifold direction caused by the ill-conditioning in widely used first-order optimizers like gradient descent. The poor convergence then acts as a source of adversarial vulnerability when the dataset is inseparable in the on-manifold direction. We provide theoretical results for logistic regression and a 2-layer linear network on the considered data distribution. Furthermore, we advocate using second-order methods that are immune to ill-conditioning and lead to better robustness. We perform experiments and exhibit tremendous robustness improvements in clean training through long training and the employment of second-order methods, corroborating our framework. Additionally, we find the inclusion of batch-norm layers hinders such robustness gains. We attribute this to differing implicit biases between traditional and batch-normalized neural networks.

Effect of Ambient-Intrinsic Dimension Gap on Adversarial Vulnerability

The existence of adversarial attacks on machine learning models imperceptible to a human is still quite a mystery from a theoretical perspective. In this work, we introduce two notions of adversarial attacks: natural or on-manifold attacks, which are perceptible by a human/oracle, and unnatural or off-manifold attacks, which are not. We argue that the existence of the off-manifold attacks is a natural consequence of the dimension gap between the intrinsic and ambient dimensions of the data. For 2-layer ReLU networks, we prove that even though the dimension gap does not affect generalization performance on samples drawn from the observed data space, it makes the clean-trained model more vulnerable to adversarial perturbations in the off-manifold direction of the data space. Our main results provide an explicit relationship between the $\ell_2,\ell_{\infty}$ attack strength of the on/off-manifold attack and the dimension gap.

On Neural Network approximation of ideal adversarial attack and convergence of adversarial training

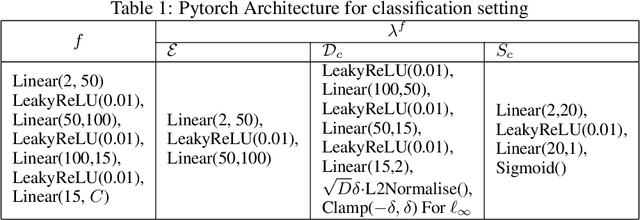
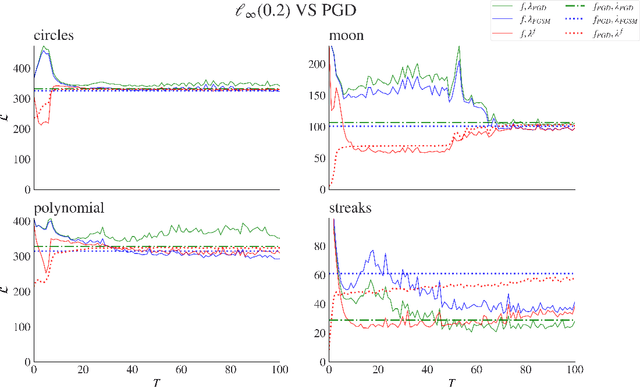
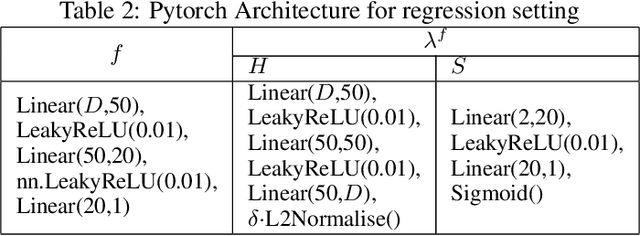
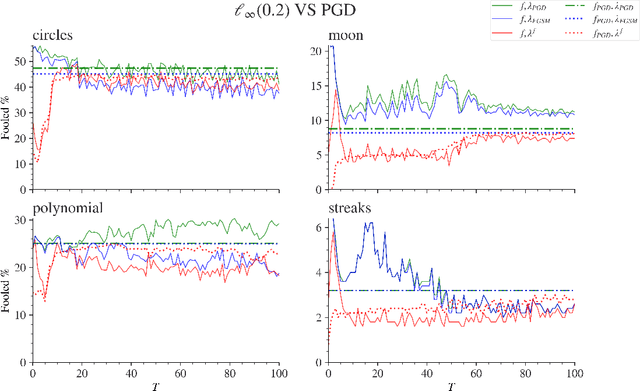
Adversarial attacks are usually expressed in terms of a gradient-based operation on the input data and model, this results in heavy computations every time an attack is generated. In this work, we solidify the idea of representing adversarial attacks as a trainable function, without further gradient computation. We first motivate that the theoretical best attacks, under proper conditions, can be represented as smooth piece-wise functions (piece-wise H\"older functions). Then we obtain an approximation result of such functions by a neural network. Subsequently, we emulate the ideal attack process by a neural network and reduce the adversarial training to a mathematical game between an attack network and a training model (a defense network). We also obtain convergence rates of adversarial loss in terms of the sample size $n$ for adversarial training in such a setting.