Raihan Kabir Ratul
Visualizing Deep Neural Networks with Topographic Activation Maps
Apr 07, 2022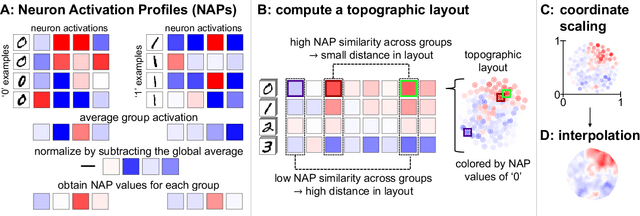


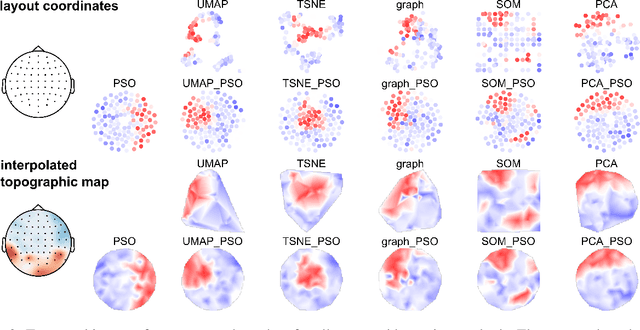
Abstract:Machine Learning with Deep Neural Networks (DNNs) has become a successful tool in solving tasks across various fields of application. The success of DNNs is strongly connected to their high complexity in terms of the number of network layers or of neurons in each layer, which severely complicates to understand how DNNs solve their learned task. To improve the explainability of DNNs, we adapt methods from neuroscience because this field has a rich experience in analyzing complex and opaque systems. In this work, we draw inspiration from how neuroscience uses topographic maps to visualize the activity of the brain when it performs certain tasks. Transferring this approach to DNNs can help to visualize and understand their internal processes more intuitively, too. However, the inner structures of brains and DNNs differ substantially. Therefore, to be able to visualize activations of neurons in DNNs as topographic maps, we research techniques to layout the neurons in a two-dimensional space in which neurons of similar activity are in the vicinity of each other. In this work, we introduce and compare different methods to obtain a topographic layout of the neurons in a network layer. Moreover, we demonstrate how to use the resulting topographic activation maps to identify errors or encoded biases in DNNs or data sets. Our novel visualization technique improves the transparency of DNN-based algorithmic decision-making systems and is accessible to a broad audience because topographic maps are intuitive to interpret without expert-knowledge in Machine Learning.
Predictive coding, precision and natural gradients
Nov 12, 2021Abstract:There is an increasing convergence between biologically plausible computational models of inference and learning with local update rules and the global gradient-based optimization of neural network models employed in machine learning. One particularly exciting connection is the correspondence between the locally informed optimization in predictive coding networks and the error backpropagation algorithm that is used to train state-of-the-art deep artificial neural networks. Here we focus on the related, but still largely under-explored connection between precision weighting in predictive coding networks and the Natural Gradient Descent algorithm for deep neural networks. Precision-weighted predictive coding is an interesting candidate for scaling up uncertainty-aware optimization -- particularly for models with large parameter spaces -- due to its distributed nature of the optimization process and the underlying local approximation of the Fisher information metric, the adaptive learning rate that is central to Natural Gradient Descent. Here, we show that hierarchical predictive coding networks with learnable precision indeed are able to solve various supervised and unsupervised learning tasks with performance comparable to global backpropagation with natural gradients and outperform their classical gradient descent counterpart on tasks where high amounts of noise are embedded in data or label inputs. When applied to unsupervised auto-encoding of image inputs, the deterministic network produces hierarchically organized and disentangled embeddings, hinting at the close connections between predictive coding and hierarchical variational inference.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge