PAC-Bayesian bounds for learning LTI-ss systems with input from empirical loss

In this paper we derive a Probably Approxilmately Correct(PAC)-Bayesian error bound for linear time-invariant (LTI) stochastic dynamical systems with inputs. Such bounds are widespread in machine learning, and they are useful for characterizing the predictive power of models learned from finitely many data points. In particular, with the bound derived in this paper relates future average prediction errors with the prediction error generated by the model on the data used for learning. In turn, this allows us to provide finite-sample error bounds for a wide class of learning/system identification algorithms. Furthermore, as LTI systems are a sub-class of recurrent neural networks (RNNs), these error bounds could be a first step towards PAC-Bayesian bounds for RNNs.

Secure PAC Bayesian Regression via Real Shamir Secret Sharing

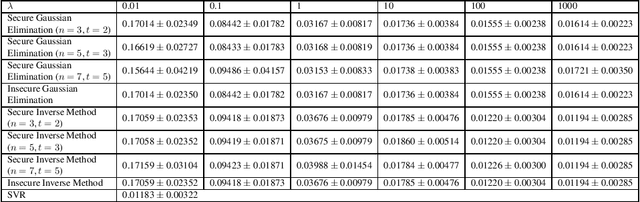
Common approach of machine learning is to generate a model by using huge amount of training data to predict the test data instances as accurate as possible. Nonetheless, concerns about data privacy are increasingly raised, but not always addressed. We present a secure protocol for obtaining a linear model relying on recently described technique called real number secret sharing. We take as our starting point the PAC Bayesian bounds and deduce a closed form for the model parameters which depends on the data and the prior from the PAC Bayesian bounds. To obtain the model parameters one need to solve a linear system. However, we consider the situation where several parties hold different data instances and they are not willing to give up the privacy of the data. Hence, we suggest to use real number secret sharing and multiparty computation to share the data and solve the linear regression in a secure way without violating the privacy of data. We suggest two methods; an inverse method and a Gaussian elimination method, and compare these methods at the end.