When Is Distributed Nonlinear Aggregation Private? Optimality and Information-Theoretical Bounds

Nonlinear aggregation is central to modern distributed systems, yet its privacy behavior is far less understood than that of linear aggregation. Unlike linear aggregation where mature mechanisms can often suppress information leakage, nonlinear operators impose inherent structural limits on what privacy guarantees are theoretically achievable when the aggregate must be computed exactly. This paper develops a unified information-theoretic framework to characterize privacy leakage in distributed nonlinear aggregation under a joint adversary that combines passive (honest-but-curious) corruption and eavesdropping over communication channels. We cover two broad classes of nonlinear aggregates: order-based operators (maximum/minimum and top-$K$) and robust aggregation (median/quantiles and trimmed mean). We first derive fundamental lower bounds on leakage that hold without sacrificing accuracy, thereby identifying the minimum unavoidable information revealed by the computation and the transcript. We then propose simple yet effective privacy-preserving distributed algorithms, and show that with appropriate randomized initialization and parameter choices, our proposed approaches can attach the derived optimal bounds for the considered operators. Extensive experiments validate the tightness of the bounds and demonstrate that network topology and key algorithmic parameters (including the stepsize) govern the observed leakage in line with the theoretical analysis, yielding actionable guidelines for privacy-preserving nonlinear aggregation.

Privacy-Preserving Distributed Expectation Maximization for Gaussian Mixture Model using Subspace Perturbation

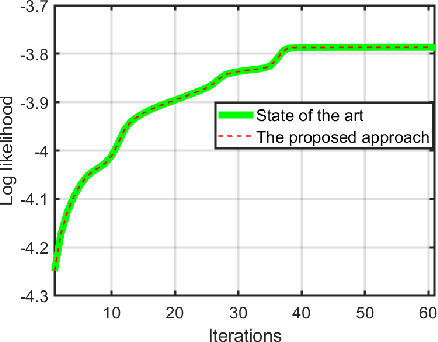
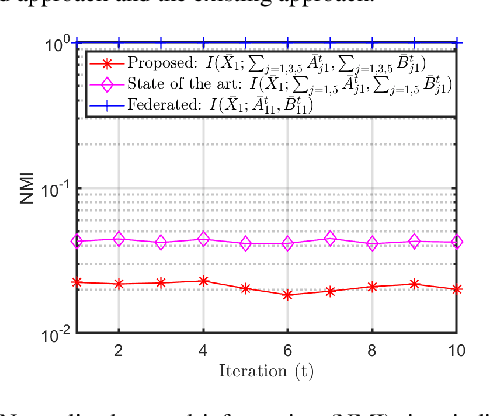
Privacy has become a major concern in machine learning. In fact, the federated learning is motivated by the privacy concern as it does not allow to transmit the private data but only intermediate updates. However, federated learning does not always guarantee privacy-preservation as the intermediate updates may also reveal sensitive information. In this paper, we give an explicit information-theoretical analysis of a federated expectation maximization algorithm for Gaussian mixture model and prove that the intermediate updates can cause severe privacy leakage. To address the privacy issue, we propose a fully decentralized privacy-preserving solution, which is able to securely compute the updates in each maximization step. Additionally, we consider two different types of security attacks: the honest-but-curious and eavesdropping adversary models. Numerical validation shows that the proposed approach has superior performance compared to the existing approach in terms of both the accuracy and privacy level.

Secure PAC Bayesian Regression via Real Shamir Secret Sharing

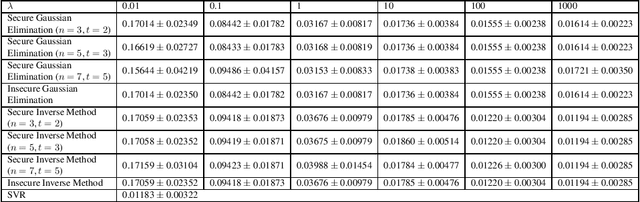
Common approach of machine learning is to generate a model by using huge amount of training data to predict the test data instances as accurate as possible. Nonetheless, concerns about data privacy are increasingly raised, but not always addressed. We present a secure protocol for obtaining a linear model relying on recently described technique called real number secret sharing. We take as our starting point the PAC Bayesian bounds and deduce a closed form for the model parameters which depends on the data and the prior from the PAC Bayesian bounds. To obtain the model parameters one need to solve a linear system. However, we consider the situation where several parties hold different data instances and they are not willing to give up the privacy of the data. Hence, we suggest to use real number secret sharing and multiparty computation to share the data and solve the linear regression in a secure way without violating the privacy of data. We suggest two methods; an inverse method and a Gaussian elimination method, and compare these methods at the end.