Rafael Bayma
Modeling and frequency domain analysis of nonlinear compliant joints for a passive dynamic swimmer
Dec 22, 2011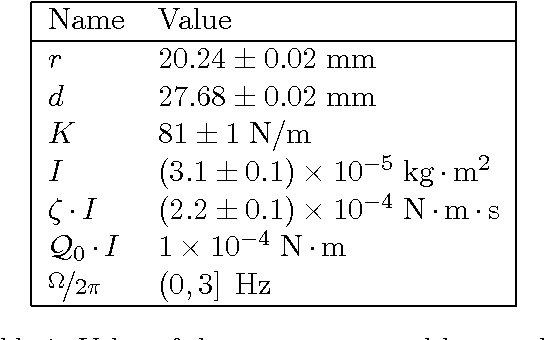
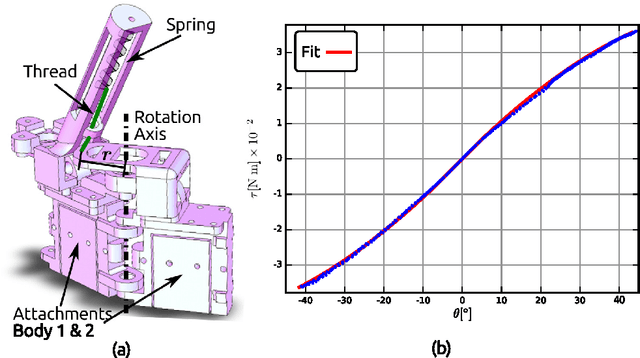
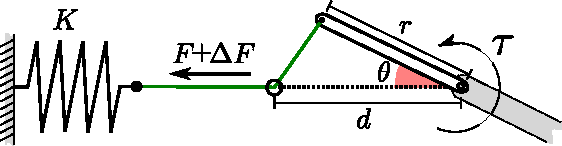
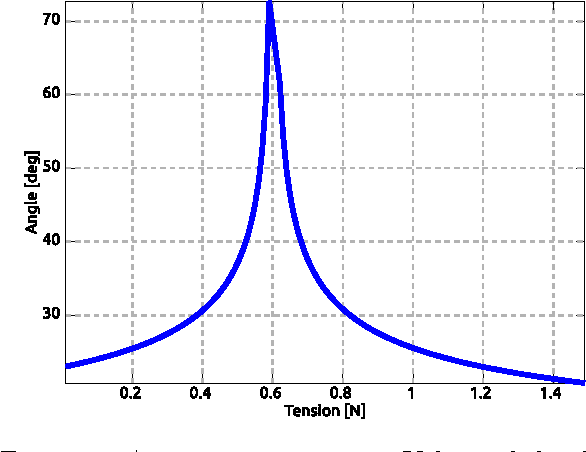
Abstract:In this paper we present the study of the mathematical model of a real life joint used in an underwater robotic fish. Fluid-structure interaction is utterly simplified and the motion of the joint is approximated by D\"uffing's equation. We compare the quality of analytical harmonic solutions previously reported, with the input-output relation obtained via truncated Volterra series expansion. Comparisons show a trade-off between accuracy and flexibility of the methods. The methods are discussed in detail in order to facilitate reproduction of our results. The approach presented herein can be used to verify results in nonlinear resonance applications and in the design of bio-inspired compliant robots that exploit passive properties of their dynamics. We focus on the potential use of this type of joint for energy extraction from environmental sources, in this case a K\'arm\'an vortex street shed by an obstacle in a flow. Open challenges and questions are mentioned throughout the document.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge