The Mathematical Game

Monte Carlo Tree Search can be used for automated theorem proving. Holophrasm is a neural theorem prover using MCTS combined with neural networks for the policy and the evaluation. In this paper we propose to improve the performance of the Holophrasm theorem prover using other game tree search algorithms.

Learning to Play Stochastic Two-player Perfect-Information Games without Knowledge

In this paper, we extend the Descent framework, which enables learning and planning in the context of two-player games with perfect information, to the framework of stochastic games. We propose two ways of doing this, the first way generalizes the search algorithm, i.e. Descent, to stochastic games and the second way approximates stochastic games by deterministic games. We then evaluate them on the game EinStein wurfelt nicht! against state-of-the-art algorithms: Expectiminimax and Polygames (i.e. the Alpha Zero algorithm). It is our generalization of Descent which obtains the best results. The approximation by deterministic games nevertheless obtains good results, presaging that it could give better results in particular contexts.

Completeness of Unbounded Best-First Game Algorithms

In this article, we prove the completeness of the following game search algorithms: unbounded best-first minimax with completion and descent with completion, i.e. we show that, with enough time, they find the best game strategy. We then generalize these two algorithms in the context of perfect information multiplayer games. We show that these generalizations are also complete: they find one of the equilibrium points.

Minimax Strikes Back

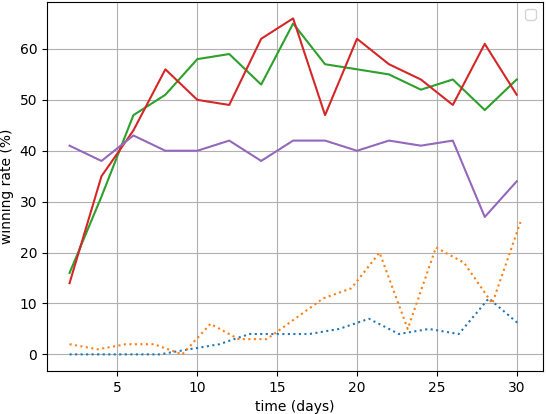
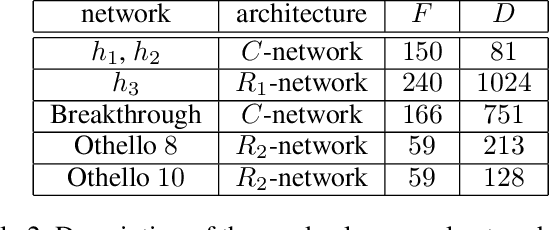
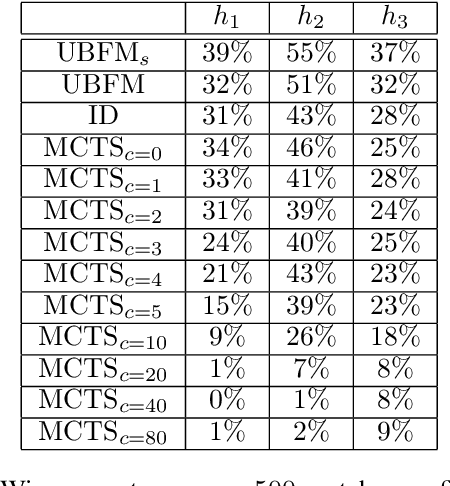
Deep Reinforcement Learning (DRL) reaches a superhuman level of play in many complete information games. The state of the art search algorithm used in combination with DRL is Monte Carlo Tree Search (MCTS). We take another approach to DRL using a Minimax algorithm instead of MCTS and learning only the evaluation of states, not the policy. We show that for multiple games it is competitive with the state of the art DRL for the learning performances and for the confrontations.

Learning to Play Two-Player Perfect-Information Games without Knowledge

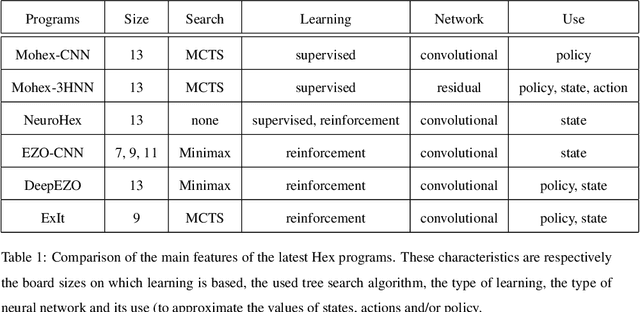
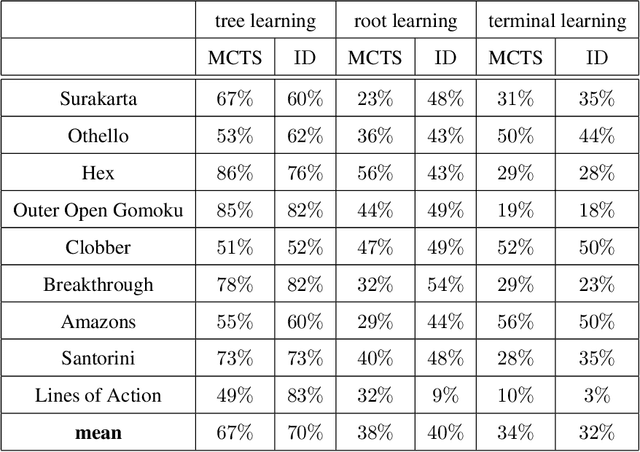
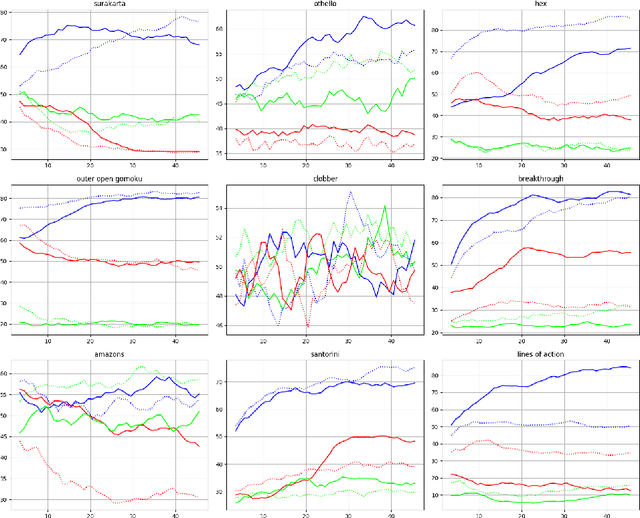
In this paper, several techniques for learning game state evaluation functions by reinforcement are proposed. The first is a generalization of tree bootstrapping (tree learning): it is adapted to the context of reinforcement learning without knowledge based on non-linear functions. With this technique, no information is lost during the reinforcement learning process. The second is a modification of minimax with unbounded depth extending the best sequences of actions to the terminal states. This modified search is intended to be used during the learning process. The third is to replace the classic gain of a game (+1 / -1) with a reinforcement heuristic. We study particular reinforcement heuristics such as: quick wins and slow defeats ; scoring ; mobility or presence. The four is another variant of unbounded minimax, which plays the safest action instead of playing the best action. This modified search is intended to be used after the learning process. The five is a new action selection distribution. The conducted experiments suggest that these techniques improve the level of play. Finally, we apply these different techniques to design program-players to the game of Hex (size 11 and 13) surpassing the level of Mohex 2.0 with reinforcement learning from self-play without knowledge. At Hex size 11 (without swap), the program-player reaches the level of Mohex 3HNN.

Tractable Fragments of Temporal Sequences of Topological Information

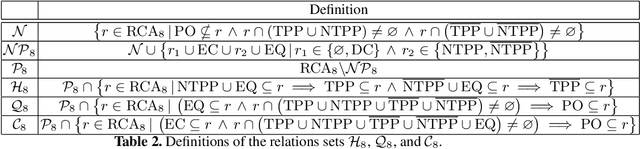
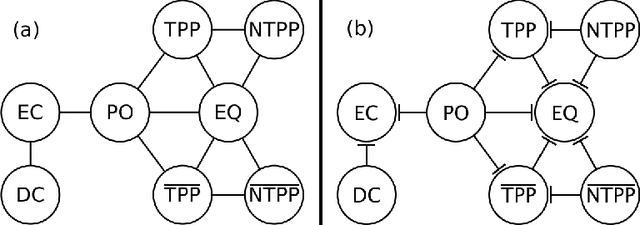
In this paper, we focus on qualitative temporal sequences of topological information. We firstly consider the context of topological temporal sequences of length greater than 3 describing the evolution of regions at consecutive time points. We show that there is no Cartesian subclass containing all the basic relations and the universal relation for which the algebraic closure decides satisfiability. However, we identify some tractable subclasses, by giving up the relations containing the non-tangential proper part relation and not containing the tangential proper part relation. We then formalize an alternative semantics for temporal sequences. We place ourselves in the context of the topological temporal sequences describing the evolution of regions on a partition of time (i.e. an alternation of instants and intervals). In this context, we identify large tractable fragments.