Tractable Fragments of Temporal Sequences of Topological Information
Paper and Code
Jul 15, 2020
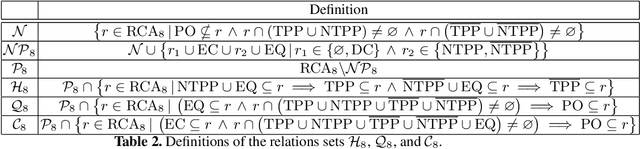
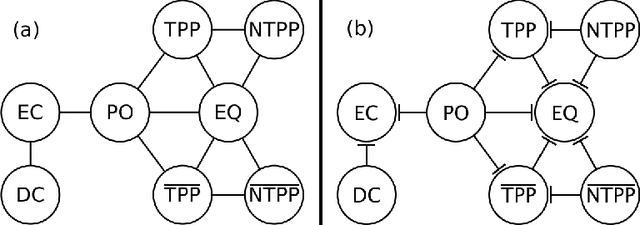

In this paper, we focus on qualitative temporal sequences of topological information. We firstly consider the context of topological temporal sequences of length greater than 3 describing the evolution of regions at consecutive time points. We show that there is no Cartesian subclass containing all the basic relations and the universal relation for which the algebraic closure decides satisfiability. However, we identify some tractable subclasses, by giving up the relations containing the non-tangential proper part relation and not containing the tangential proper part relation. We then formalize an alternative semantics for temporal sequences. We place ourselves in the context of the topological temporal sequences describing the evolution of regions on a partition of time (i.e. an alternation of instants and intervals). In this context, we identify large tractable fragments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge