Learning to Play Two-Player Perfect-Information Games without Knowledge

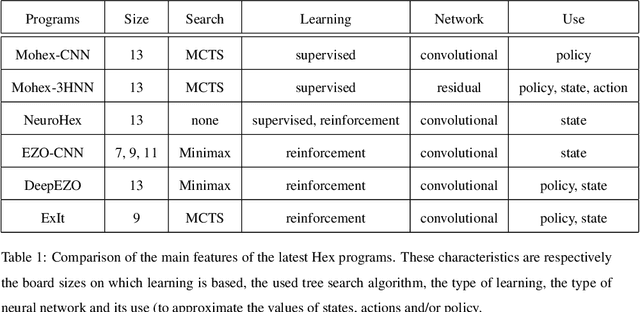
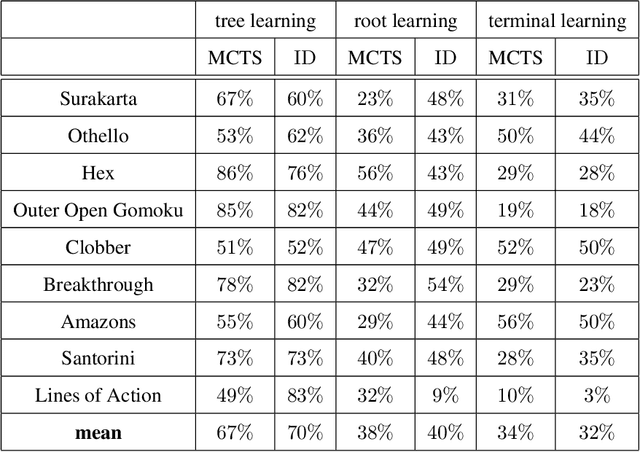
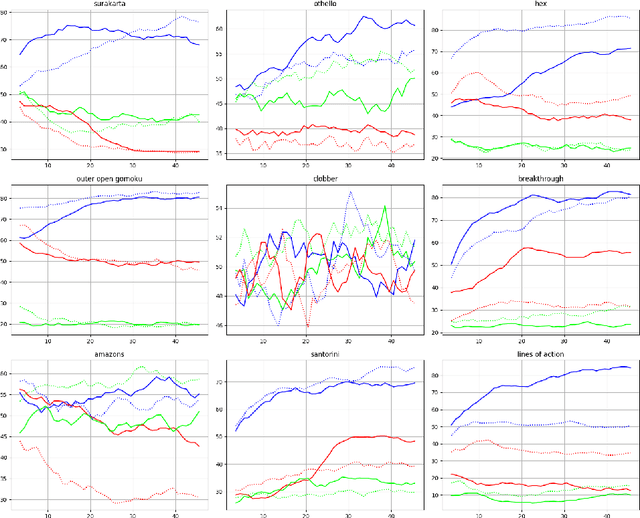
In this paper, several techniques for learning game state evaluation functions by reinforcement are proposed. The first is a generalization of tree bootstrapping (tree learning): it is adapted to the context of reinforcement learning without knowledge based on non-linear functions. With this technique, no information is lost during the reinforcement learning process. The second is a modification of minimax with unbounded depth extending the best sequences of actions to the terminal states. This modified search is intended to be used during the learning process. The third is to replace the classic gain of a game (+1 / -1) with a reinforcement heuristic. We study particular reinforcement heuristics such as: quick wins and slow defeats ; scoring ; mobility or presence. The four is another variant of unbounded minimax, which plays the safest action instead of playing the best action. This modified search is intended to be used after the learning process. The five is a new action selection distribution. The conducted experiments suggest that these techniques improve the level of play. Finally, we apply these different techniques to design program-players to the game of Hex (size 11 and 13) surpassing the level of Mohex 2.0 with reinforcement learning from self-play without knowledge. At Hex size 11 (without swap), the program-player reaches the level of Mohex 3HNN.