A note on patch-based low-rank minimization for fast image denoising

Patch-based low-rank minimization for image processing attracts much attention in recent years. The minimization of the matrix rank coupled with the Frobenius norm data fidelity can be solved by the hard thresholding filter with principle component analysis (PCA) or singular value decomposition (SVD). Based on this idea, we propose a patch-based low-rank minimization method for image denoising. The main denoising process is stated in three equivalent way: PCA, SVD and low-rank minimization. Compared to recent patch-based sparse representation methods, experiments demonstrate that the proposed method is rather rapid, and it is effective for a variety of natural grayscale images and color images, especially for texture parts in images. Further improvements of this method are also given. In addition, due to the simplicity of this method, we could provide an explanation of the choice of the threshold parameter, estimation of PSNR values, and give other insights into this method.

Removing Mixture of Gaussian and Impulse Noise by Patch-Based Weighted Means

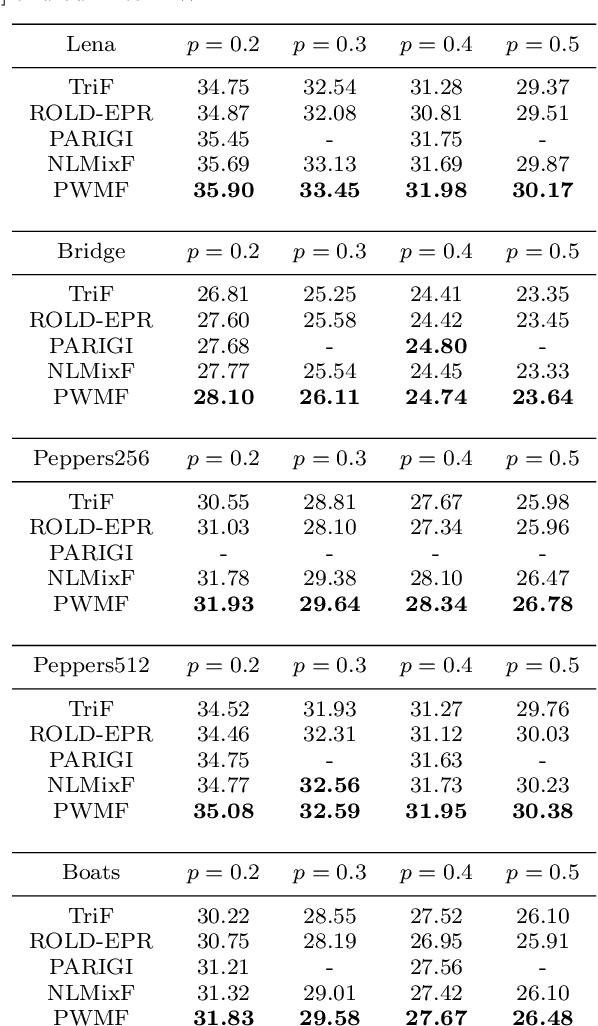
We first establish a law of large numbers and a convergence theorem in distribution to show the rate of convergence of the non-local means filter for removing Gaussian noise. We then introduce the notion of degree of similarity to measure the role of similarity for the non-local means filter. Based on the convergence theorems, we propose a patch-based weighted means filter for removing impulse noise and its mixture with Gaussian noise by combining the essential idea of the trilateral filter and that of the non-local means filter. Our experiments show that our filter is competitive compared to recently proposed methods.

A Non-Local Means Filter for Removing the Poisson Noise

A new image denoising algorithm to deal with the Poisson noise model is given, which is based on the idea of Non-Local Mean. By using the "Oracle" concept, we establish a theorem to show that the Non-Local Means Filter can effectively deal with Poisson noise with some modification. Under the theoretical result, we construct our new algorithm called Non-Local Means Poisson Filter and demonstrate in theory that the filter converges at the usual optimal rate. The filter is as simple as the classic Non-Local Means and the simulation results show that our filter is very competitive.

Optimal Weights Mixed Filter for Removing Mixture of Gaussian and Impulse Noises

According to the character of Gaussian, we modify the Rank-Ordered Absolute Differences (ROAD) to Rank-Ordered Absolute Differences of mixture of Gaussian and impulse noises (ROADG). It will be more effective to detect impulse noise when the impulse is mixed with Gaussian noise. Combining rightly the ROADG with Optimal Weights Filter (OWF), we obtain a new method to deal with the mixed noise, called Optimal Weights Mixed Filter (OWMF). The simulation results show that the method is effective to remove the mixed noise.

Controlled Total Variation regularization for inverse problems

This paper provides a new algorithm for solving inverse problems, based on the minimization of the $L^2$ norm and on the control of the Total Variation. It consists in relaxing the role of the Total Variation in the classical Total Variation minimization approach, which permits us to get better approximation to the inverse problems. The numerical results on the deconvolution problem show that our method outperforms some previous ones.