Doubly-Irregular Repeat-Accumulate Codes over Integer Rings for Multi-user Communications

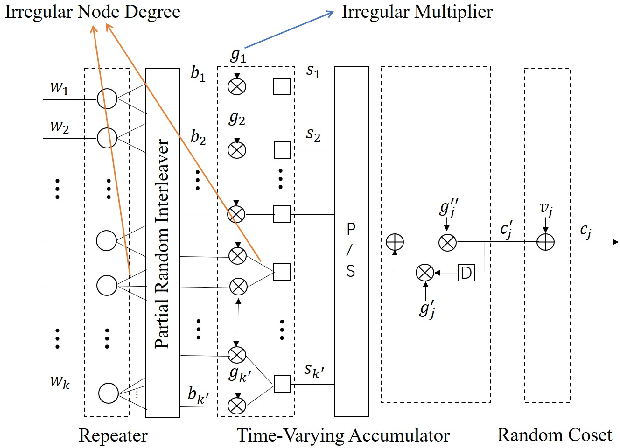
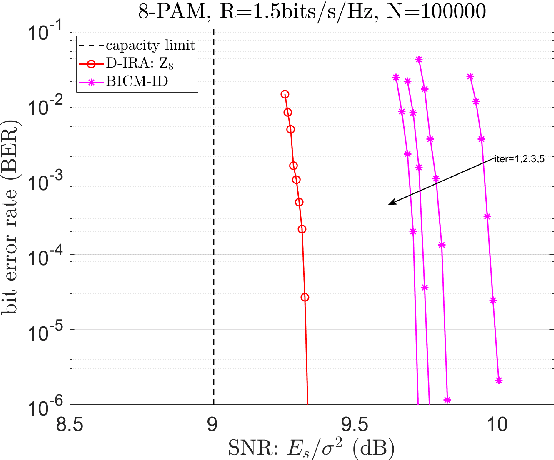
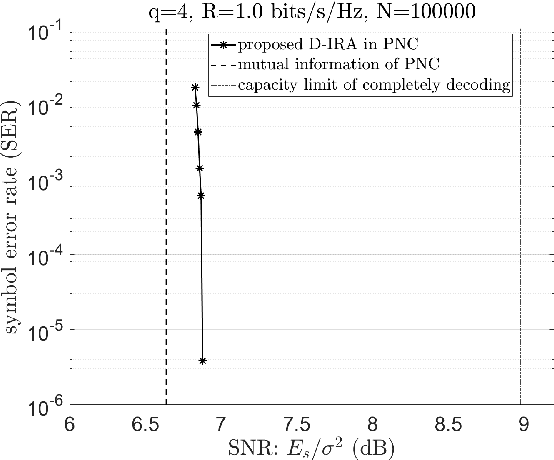
Structured codes based on lattices were shown to provide enlarged capacity for multi-user communication networks. In this paper, we study capacity-approaching irregular repeat accumulate (IRA) codes over integer rings $\mathbb{Z}_{2^{m}}$ for $2^m$-PAM signaling, $m=1,2,\cdots$. Such codes feature the property that the integer sum of $K$ codewords belongs to the extended codebook (or lattice) w.r.t. the base code. With it, \emph{% structured binning} can be utilized and the gains promised in lattice based network information theory can be materialized in practice. In designing IRA ring codes, we first analyze the effect of zero-divisors of integer ring on the iterative belief-propagation (BP) decoding, and show the invalidity of symmetric Gaussian approximation. Then we propose a doubly IRA (D-IRA) ring code structure, consisting of \emph{irregular multiplier distribution} and \emph{irregular node-degree distribution}, that can restore the symmetry and optimize the BP decoding threshold. For point-to-point AWGN channel with $% 2^m $-PAM inputs, D-IRA ring codes perform as low as 0.29 dB to the capacity limits, outperforming existing bit-interleaved coded-modulation (BICM) and IRA modulation codes over GF($2^m$). We then proceed to design D-IRA ring codes for two important multi-user communication setups, namely compute-forward (CF) and dirty paper coding (DPC), with $2^m$-PAM signaling. With it, a physical-layer network coding scheme yields a gap to the CF limit by 0.24 dB, and a simple linear DPC scheme exhibits a gap to the capacity by 0.91 dB.

On Lattice-Code based Multiple Access: Uplink Architecture and Algorithms

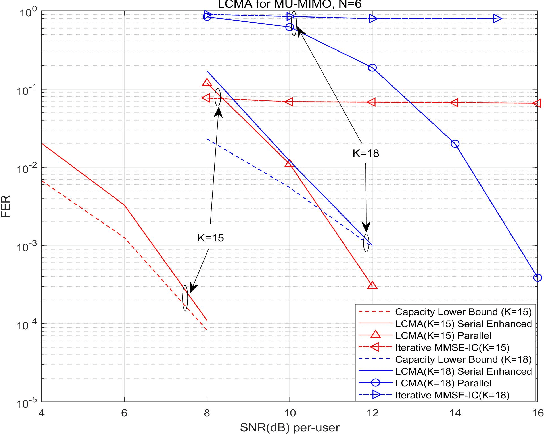
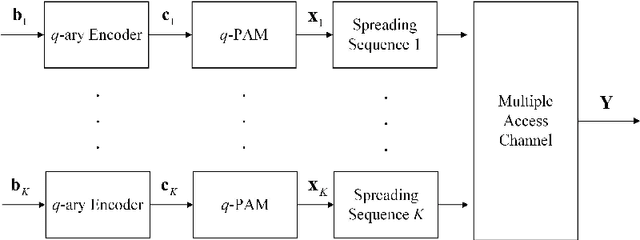
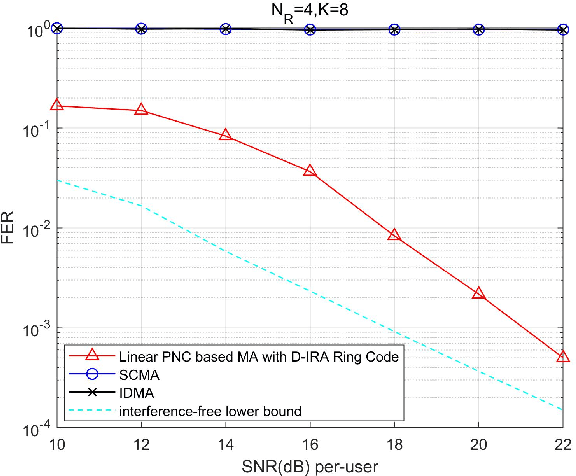
This paper studies a lattice-code based multiple-access (LCMA) framework, and develops a package of processing techniques that are essential to its practical implementation. In the uplink, $K$ users encode their messages with the same ring coded modulation of $2^{m}$-PAM signaling. With it, the integer sum of multiple codewords belongs to the $n$-dimension lattice of the base code. Such property enables efficient \textit{algebraic binning} for computing linear combinations of $K$ users' messages. For the receiver, we devise two new algorithms, based on linear physical-layer network coding and linear filtering, to calculate the symbol-wise a posteriori probabilities (APPs) w.r.t. the $K$ streams of linear codeword combinations. The resultant APP streams are forwarded to the $q$-ary belief-propagation decoders, which parallelly compute $K$ streams of linear message combinations. Finally, by multiplying the inverse of the coefficient matrix, all users' messages are recovered. Even with single-stage parallel processing, LCMA is shown to support a remarkably larger number of users and exhibits improved frame error rate (FER) relative to existing NOMA systems such as IDMA and SCMA. Further, we propose a new multi-stage LCMA receiver relying on \emph{generalized matrix inversion}. With it, a near-capacity performance is demonstrated for a wide range of system loads. Numerical results demonstrate that the number of users that LCMA can support is no less than 350\% of the length of the spreading sequence or number of receive antennas. Since LCMA relaxes receiver iteration, off-the-shelf channel codes in standards can be directly utilized, avoiding the compatibility and convergence issue of channel code and detector in IDMA and SCMA.