Fangtao Yu
Doubly-Irregular Repeat-Accumulate Codes over Integer Rings for Multi-user Communications
Oct 04, 2022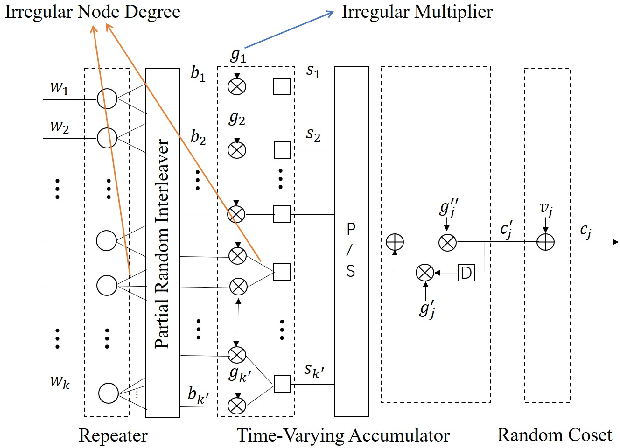
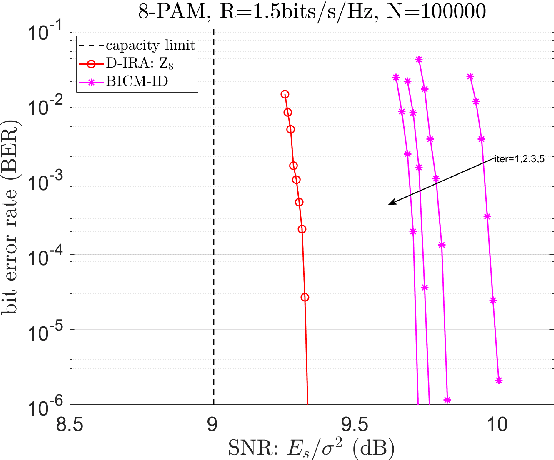
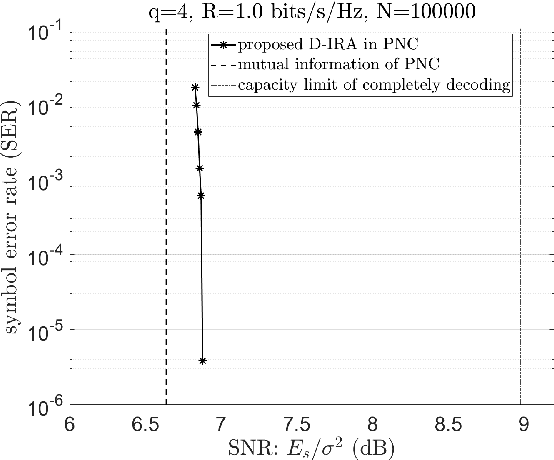
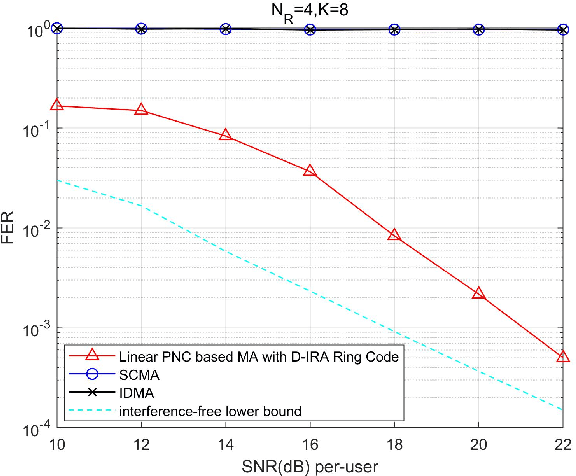
Abstract:Structured codes based on lattices were shown to provide enlarged capacity for multi-user communication networks. In this paper, we study capacity-approaching irregular repeat accumulate (IRA) codes over integer rings $\mathbb{Z}_{2^{m}}$ for $2^m$-PAM signaling, $m=1,2,\cdots$. Such codes feature the property that the integer sum of $K$ codewords belongs to the extended codebook (or lattice) w.r.t. the base code. With it, \emph{% structured binning} can be utilized and the gains promised in lattice based network information theory can be materialized in practice. In designing IRA ring codes, we first analyze the effect of zero-divisors of integer ring on the iterative belief-propagation (BP) decoding, and show the invalidity of symmetric Gaussian approximation. Then we propose a doubly IRA (D-IRA) ring code structure, consisting of \emph{irregular multiplier distribution} and \emph{irregular node-degree distribution}, that can restore the symmetry and optimize the BP decoding threshold. For point-to-point AWGN channel with $% 2^m $-PAM inputs, D-IRA ring codes perform as low as 0.29 dB to the capacity limits, outperforming existing bit-interleaved coded-modulation (BICM) and IRA modulation codes over GF($2^m$). We then proceed to design D-IRA ring codes for two important multi-user communication setups, namely compute-forward (CF) and dirty paper coding (DPC), with $2^m$-PAM signaling. With it, a physical-layer network coding scheme yields a gap to the CF limit by 0.24 dB, and a simple linear DPC scheme exhibits a gap to the capacity by 0.91 dB.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge