On Lattice-Code based Multiple Access: Uplink Architecture and Algorithms
Paper and Code
Oct 03, 2022
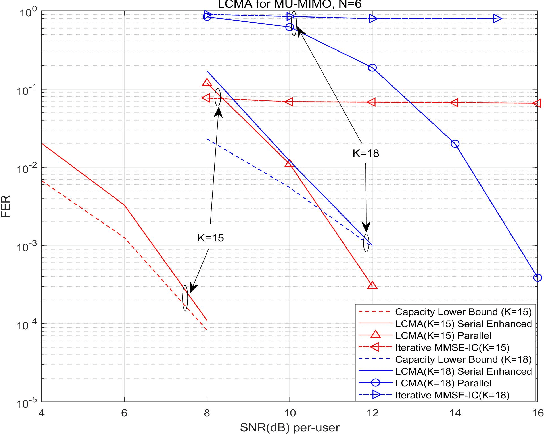

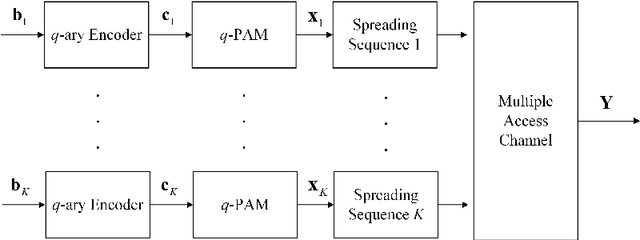
This paper studies a lattice-code based multiple-access (LCMA) framework, and develops a package of processing techniques that are essential to its practical implementation. In the uplink, $K$ users encode their messages with the same ring coded modulation of $2^{m}$-PAM signaling. With it, the integer sum of multiple codewords belongs to the $n$-dimension lattice of the base code. Such property enables efficient \textit{algebraic binning} for computing linear combinations of $K$ users' messages. For the receiver, we devise two new algorithms, based on linear physical-layer network coding and linear filtering, to calculate the symbol-wise a posteriori probabilities (APPs) w.r.t. the $K$ streams of linear codeword combinations. The resultant APP streams are forwarded to the $q$-ary belief-propagation decoders, which parallelly compute $K$ streams of linear message combinations. Finally, by multiplying the inverse of the coefficient matrix, all users' messages are recovered. Even with single-stage parallel processing, LCMA is shown to support a remarkably larger number of users and exhibits improved frame error rate (FER) relative to existing NOMA systems such as IDMA and SCMA. Further, we propose a new multi-stage LCMA receiver relying on \emph{generalized matrix inversion}. With it, a near-capacity performance is demonstrated for a wide range of system loads. Numerical results demonstrate that the number of users that LCMA can support is no less than 350\% of the length of the spreading sequence or number of receive antennas. Since LCMA relaxes receiver iteration, off-the-shelf channel codes in standards can be directly utilized, avoiding the compatibility and convergence issue of channel code and detector in IDMA and SCMA.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge