Zeroth-Order Policy Gradient for Reinforcement Learning from Human Feedback without Reward Inference

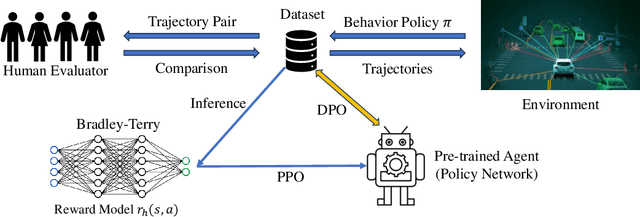
Reward inference (learning a reward model from human preferences) is a critical intermediate step in Reinforcement Learning from Human Feedback (RLHF) for fine-tuning Large Language Models (LLMs) such as ChatGPT. In practice, reward inference faces several fundamental challenges, including double problem misspecification, reward model evaluation without ground truth, distribution shift, and overfitting in joint reward model and policy training. An alternative approach that avoids these pitfalls is direct policy optimization without reward inference, such as Direct Preference Optimization (DPO), which provides a much simpler pipeline and has shown empirical success in LLMs. However, DPO utilizes the closed-form expression between the optimal policy and the reward function, which only works under the bandit setting or deterministic MDPs. This paper develops two RLHF algorithms without reward inference, which work for general RL problems beyond bandits and deterministic MDPs, and general preference models beyond the Bradely-Terry model. The key idea is to estimate the local value function difference from human preferences and then approximate the policy gradient with a zeroth-order gradient approximator. For both algorithms, we establish rates of convergence in terms of the number of policy gradient iterations, as well as the number of trajectory samples and human preference queries per iteration. Our results show there exist provably efficient methods to solve general RLHF problems without reward inference.

Cost Aware Best Arm Identification

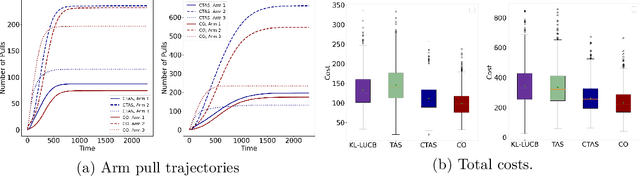
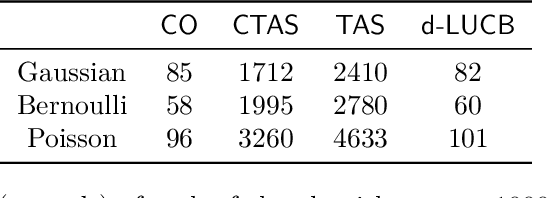
In this paper, we study a best arm identification problem with dual objects. In addition to the classic reward, each arm is associated with a cost distribution and the goal is to identify the largest reward arm using the minimum expected cost. We call it \emph{Cost Aware Best Arm Identification} (CABAI), which captures the separation of testing and implementation phases in product development pipelines and models the objective shift between phases, i.e., cost for testing and reward for implementation. We first derive an theoretic lower bound for CABAI and propose an algorithm called $\mathsf{CTAS}$ to match it asymptotically. To reduce the computation of $\mathsf{CTAS}$, we further propose a low-complexity algorithm called CO, based on a square-root rule, which proves optimal in simplified two-armed models and generalizes surprisingly well in numerical experiments. Our results show (i) ignoring the heterogeneous action cost results in sub-optimality in practice, and (ii) low-complexity algorithms deliver near-optimal performance over a wide range of problems.

Fast and Regret Optimal Best Arm Identification: Fundamental Limits and Low-Complexity Algorithms

This paper considers a stochastic multi-armed bandit (MAB) problem with dual objectives: (i) quick identification and commitment to the optimal arm, and (ii) reward maximization throughout a sequence of $T$ consecutive rounds. Though each objective has been individually well-studied, i.e., best arm identification for (i) and regret minimization for (ii), the simultaneous realization of both objectives remains an open problem, despite its practical importance. This paper introduces \emph{Regret Optimal Best Arm Identification} (ROBAI) which aims to achieve these dual objectives. To solve ROBAI with both pre-determined stopping time and adaptive stopping time requirements, we present the $\mathsf{EOCP}$ algorithm and its variants respectively, which not only achieve asymptotic optimal regret in both Gaussian and general bandits, but also commit to the optimal arm in $\mathcal{O}(\log T)$ rounds with pre-determined stopping time and $\mathcal{O}(\log^2 T)$ rounds with adaptive stopping time. We further characterize lower bounds on the commitment time (equivalent to sample complexity) of ROBAI, showing that $\mathsf{EOCP}$ and its variants are sample optimal with pre-determined stopping time, and almost sample optimal with adaptive stopping time. Numerical results confirm our theoretical analysis and reveal an interesting ``over-exploration'' phenomenon carried by classic $\mathsf{UCB}$ algorithms, such that $\mathsf{EOCP}$ has smaller regret even though it stops exploration much earlier than $\mathsf{UCB}$ ($\mathcal{O}(\log T)$ versus $\mathcal{O}(T)$), which suggests over-exploration is unnecessary and potentially harmful to system performance.