Kellen Kanarios
Cost Aware Best Arm Identification
Feb 26, 2024

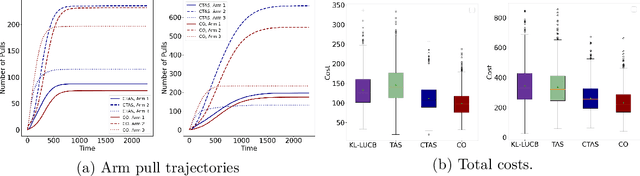
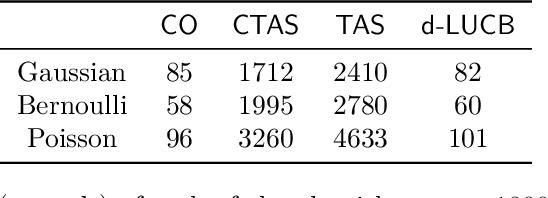
Abstract:In this paper, we study a best arm identification problem with dual objects. In addition to the classic reward, each arm is associated with a cost distribution and the goal is to identify the largest reward arm using the minimum expected cost. We call it \emph{Cost Aware Best Arm Identification} (CABAI), which captures the separation of testing and implementation phases in product development pipelines and models the objective shift between phases, i.e., cost for testing and reward for implementation. We first derive an theoretic lower bound for CABAI and propose an algorithm called $\mathsf{CTAS}$ to match it asymptotically. To reduce the computation of $\mathsf{CTAS}$, we further propose a low-complexity algorithm called CO, based on a square-root rule, which proves optimal in simplified two-armed models and generalizes surprisingly well in numerical experiments. Our results show (i) ignoring the heterogeneous action cost results in sub-optimality in practice, and (ii) low-complexity algorithms deliver near-optimal performance over a wide range of problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge