Zeroth-Order Policy Gradient for Reinforcement Learning from Human Feedback without Reward Inference
Paper and Code
Sep 25, 2024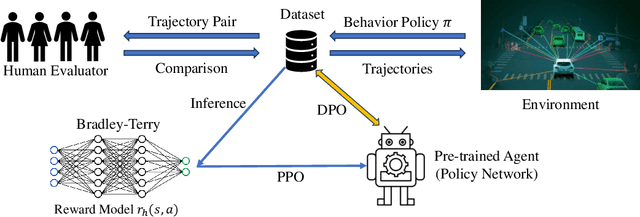
Reward inference (learning a reward model from human preferences) is a critical intermediate step in Reinforcement Learning from Human Feedback (RLHF) for fine-tuning Large Language Models (LLMs) such as ChatGPT. In practice, reward inference faces several fundamental challenges, including double problem misspecification, reward model evaluation without ground truth, distribution shift, and overfitting in joint reward model and policy training. An alternative approach that avoids these pitfalls is direct policy optimization without reward inference, such as Direct Preference Optimization (DPO), which provides a much simpler pipeline and has shown empirical success in LLMs. However, DPO utilizes the closed-form expression between the optimal policy and the reward function, which only works under the bandit setting or deterministic MDPs. This paper develops two RLHF algorithms without reward inference, which work for general RL problems beyond bandits and deterministic MDPs, and general preference models beyond the Bradely-Terry model. The key idea is to estimate the local value function difference from human preferences and then approximate the policy gradient with a zeroth-order gradient approximator. For both algorithms, we establish rates of convergence in terms of the number of policy gradient iterations, as well as the number of trajectory samples and human preference queries per iteration. Our results show there exist provably efficient methods to solve general RLHF problems without reward inference.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge