The Power of Decaying Steps: Enhancing Attack Stability and Transferability for Sign-based Optimizers

Crafting adversarial examples can be formulated as an optimization problem. While sign-based optimizers such as I-FGSM and MI-FGSM have become the de facto standard for the induced optimization problems, there still exist several unsolved problems in theoretical grounding and practical reliability especially in non-convergence and instability, which inevitably influences their transferability. Contrary to the expectation, we observe that the attack success rate may degrade sharply when more number of iterations are conducted. In this paper, we address these issues from an optimization perspective. By reformulating the sign-based optimizer as a specific coordinate-wise gradient descent, we argue that one cause for non-convergence and instability is their non-decaying step-size scheduling. Based upon this viewpoint, we propose a series of new attack algorithms that enforce Monotonically Decreasing Coordinate-wise Step-sizes (MDCS) within sign-based optimizers. Typically, we further provide theoretical guarantees proving that MDCS-MI attains an optimal convergence rate of $O(1/\sqrt{T})$, where $T$ is the number of iterations. Extensive experiments on image classification and cross-modal retrieval tasks demonstrate that our approach not only significantly improves transferability but also enhances attack stability compared to state-of-the-art sign-based methods.

Optimizing the Adversarial Perturbation with a Momentum-based Adaptive Matrix

Generating adversarial examples (AEs) can be formulated as an optimization problem. Among various optimization-based attacks, the gradient-based PGD and the momentum-based MI-FGSM have garnered considerable interest. However, all these attacks use the sign function to scale their perturbations, which raises several theoretical concerns from the point of view of optimization. In this paper, we first reveal that PGD is actually a specific reformulation of the projected gradient method using only the current gradient to determine its step-size. Further, we show that when we utilize a conventional adaptive matrix with the accumulated gradients to scale the perturbation, PGD becomes AdaGrad. Motivated by this analysis, we present a novel momentum-based attack AdaMI, in which the perturbation is optimized with an interesting momentum-based adaptive matrix. AdaMI is proved to attain optimal convergence for convex problems, indicating that it addresses the non-convergence issue of MI-FGSM, thereby ensuring stability of the optimization process. The experiments demonstrate that the proposed momentum-based adaptive matrix can serve as a general and effective technique to boost adversarial transferability over the state-of-the-art methods across different networks while maintaining better stability and imperceptibility.

Adapting Step-size: A Unified Perspective to Analyze and Improve Gradient-based Methods for Adversarial Attacks

Learning adversarial examples can be formulated as an optimization problem of maximizing the loss function with some box-constraints. However, for solving this induced optimization problem, the state-of-the-art gradient-based methods such as FGSM, I-FGSM and MI-FGSM look different from their original methods especially in updating the direction, which makes it difficult to understand them and then leaves some theoretical issues to be addressed in viewpoint of optimization. In this paper, from the perspective of adapting step-size, we provide a unified theoretical interpretation of these gradient-based adversarial learning methods. We show that each of these algorithms is in fact a specific reformulation of their original gradient methods but using the step-size rules with only current gradient information. Motivated by such analysis, we present a broad class of adaptive gradient-based algorithms based on the regular gradient methods, in which the step-size strategy utilizing information of the accumulated gradients is integrated. Such adaptive step-size strategies directly normalize the scale of the gradients rather than use some empirical operations. The important benefit is that convergence for the iterative algorithms is guaranteed and then the whole optimization process can be stabilized. The experiments demonstrate that our AdaI-FGM consistently outperforms I-FGSM and AdaMI-FGM remains competitive with MI-FGSM for black-box attacks.

The Role of Momentum Parameters in the Optimal Convergence of Adaptive Polyak's Heavy-ball Methods

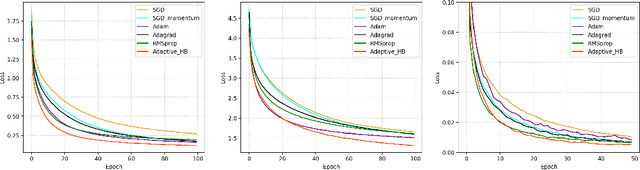
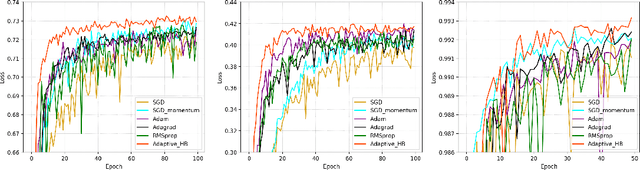
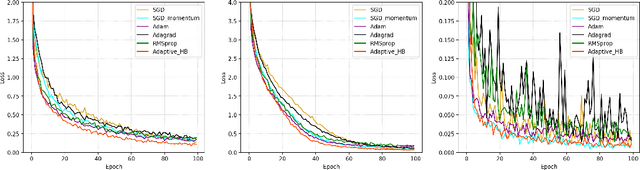
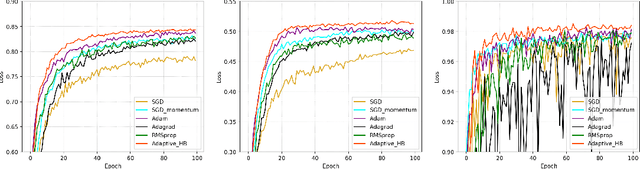
The adaptive stochastic gradient descent (SGD) with momentum has been widely adopted in deep learning as well as convex optimization. In practice, the last iterate is commonly used as the final solution to make decisions. However, the available regret analysis and the setting of constant momentum parameters only guarantee the optimal convergence of the averaged solution. In this paper, we fill this theory-practice gap by investigating the convergence of the last iterate (referred to as individual convergence), which is a more difficult task than convergence analysis of the averaged solution. Specifically, in the constrained convex cases, we prove that the adaptive Polyak's Heavy-ball (HB) method, in which only the step size is updated using the exponential moving average strategy, attains an optimal individual convergence rate of $O(\frac{1}{\sqrt{t}})$, as opposed to the optimality of $O(\frac{\log t}{\sqrt {t}})$ of SGD, where $t$ is the number of iterations. Our new analysis not only shows how the HB momentum and its time-varying weight help us to achieve the acceleration in convex optimization but also gives valuable hints how the momentum parameters should be scheduled in deep learning. Empirical results on optimizing convex functions and training deep networks validate the correctness of our convergence analysis and demonstrate the improved performance of the adaptive HB methods.

Gradient Descent Averaging and Primal-dual Averaging for Strongly Convex Optimization

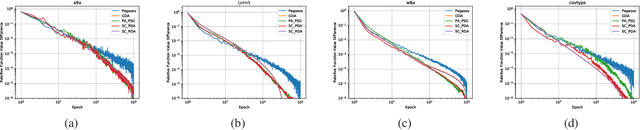
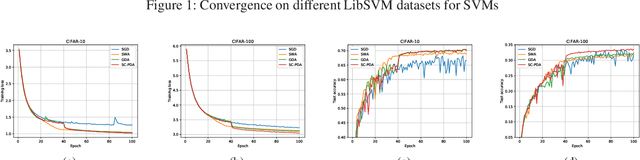
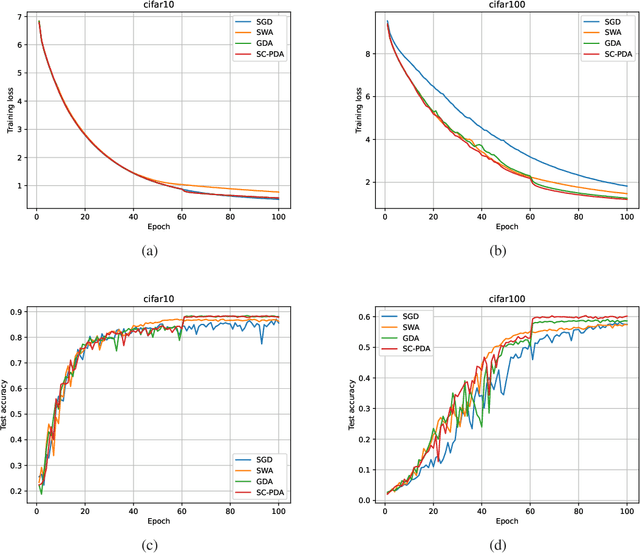
Averaging scheme has attracted extensive attention in deep learning as well as traditional machine learning. It achieves theoretically optimal convergence and also improves the empirical model performance. However, there is still a lack of sufficient convergence analysis for strongly convex optimization. Typically, the convergence about the last iterate of gradient descent methods, which is referred to as individual convergence, fails to attain its optimality due to the existence of logarithmic factor. In order to remove this factor, we first develop gradient descent averaging (GDA), which is a general projection-based dual averaging algorithm in the strongly convex setting. We further present primal-dual averaging for strongly convex cases (SC-PDA), where primal and dual averaging schemes are simultaneously utilized. We prove that GDA yields the optimal convergence rate in terms of output averaging, while SC-PDA derives the optimal individual convergence. Several experiments on SVMs and deep learning models validate the correctness of theoretical analysis and effectiveness of algorithms.