Scale Invariance of Graph Neural Networks

We address two fundamental challenges in Graph Neural Networks (GNNs): (1) the lack of theoretical support for invariance learning, a critical property in image processing, and (2) the absence of a unified model capable of excelling on both homophilic and heterophilic graph datasets. To tackle these issues, we establish and prove scale invariance in graphs, extending this key property to graph learning, and validate it through experiments on real-world datasets. Leveraging directed multi-scaled graphs and an adaptive self-loop strategy, we propose ScaleNet, a unified network architecture that achieves state-of-the-art performance across four homophilic and two heterophilic benchmark datasets. Furthermore, we show that through graph transformation based on scale invariance, uniform weights can replace computationally expensive edge weights in digraph inception networks while maintaining or improving performance. For another popular GNN approach to digraphs, we demonstrate the equivalence between Hermitian Laplacian methods and GraphSAGE with incidence normalization. ScaleNet bridges the gap between homophilic and heterophilic graph learning, offering both theoretical insights into scale invariance and practical advancements in unified graph learning. Our implementation is publicly available at https://github.com/Qin87/ScaleNet/tree/Aug23.

ScaleNet: Scale Invariance Learning in Directed Graphs

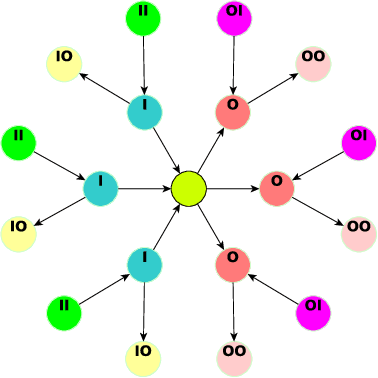
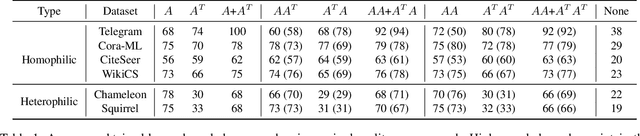
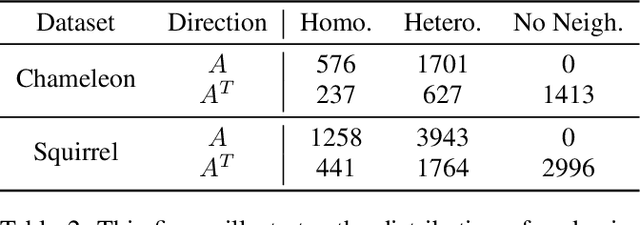
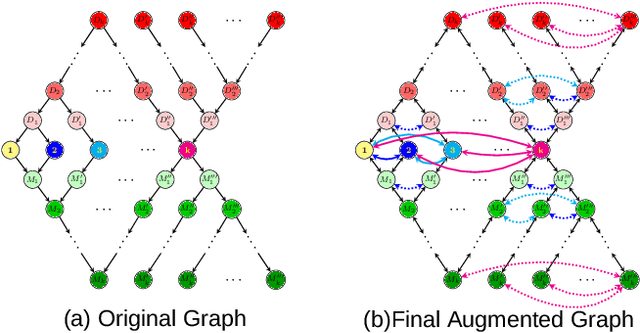
Graph Neural Networks (GNNs) have advanced relational data analysis but lack invariance learning techniques common in image classification. In node classification with GNNs, it is actually the ego-graph of the center node that is classified. This research extends the scale invariance concept to node classification by drawing an analogy to image processing: just as scale invariance being used in image classification to capture multi-scale features, we propose the concept of ``scaled ego-graphs''. Scaled ego-graphs generalize traditional ego-graphs by replacing undirected single-edges with ``scaled-edges'', which are ordered sequences of multiple directed edges. We empirically assess the performance of the proposed scale invariance in graphs on seven benchmark datasets, across both homophilic and heterophilic structures. Our scale-invariance-based graph learning outperforms inception models derived from random walks by being simpler, faster, and more accurate. The scale invariance explains inception models' success on homophilic graphs and limitations on heterophilic graphs. To ensure applicability of inception model to heterophilic graphs as well, we further present ScaleNet, an architecture that leverages multi-scaled features. ScaleNet achieves state-of-the-art results on five out of seven datasets (four homophilic and one heterophilic) and matches top performance on the remaining two, demonstrating its excellent applicability. This represents a significant advance in graph learning, offering a unified framework that enhances node classification across various graph types. Our code is available at https://github.com/Qin87/ScaleNet/tree/July25.