Qichao Que
Revisiting Kernelized Locality-Sensitive Hashing for Improved Large-Scale Image Retrieval
Nov 16, 2014



Abstract:We present a simple but powerful reinterpretation of kernelized locality-sensitive hashing (KLSH), a general and popular method developed in the vision community for performing approximate nearest-neighbor searches in an arbitrary reproducing kernel Hilbert space (RKHS). Our new perspective is based on viewing the steps of the KLSH algorithm in an appropriately projected space, and has several key theoretical and practical benefits. First, it eliminates the problematic conceptual difficulties that are present in the existing motivation of KLSH. Second, it yields the first formal retrieval performance bounds for KLSH. Third, our analysis reveals two techniques for boosting the empirical performance of KLSH. We evaluate these extensions on several large-scale benchmark image retrieval data sets, and show that our analysis leads to improved recall performance of at least 12%, and sometimes much higher, over the standard KLSH method.
Inverse Density as an Inverse Problem: The Fredholm Equation Approach
Apr 25, 2013


Abstract:In this paper we address the problem of estimating the ratio $\frac{q}{p}$ where $p$ is a density function and $q$ is another density, or, more generally an arbitrary function. Knowing or approximating this ratio is needed in various problems of inference and integration, in particular, when one needs to average a function with respect to one probability distribution, given a sample from another. It is often referred as {\it importance sampling} in statistical inference and is also closely related to the problem of {\it covariate shift} in transfer learning as well as to various MCMC methods. It may also be useful for separating the underlying geometry of a space, say a manifold, from the density function defined on it. Our approach is based on reformulating the problem of estimating $\frac{q}{p}$ as an inverse problem in terms of an integral operator corresponding to a kernel, and thus reducing it to an integral equation, known as the Fredholm problem of the first kind. This formulation, combined with the techniques of regularization and kernel methods, leads to a principled kernel-based framework for constructing algorithms and for analyzing them theoretically. The resulting family of algorithms (FIRE, for Fredholm Inverse Regularized Estimator) is flexible, simple and easy to implement. We provide detailed theoretical analysis including concentration bounds and convergence rates for the Gaussian kernel in the case of densities defined on $\R^d$, compact domains in $\R^d$ and smooth $d$-dimensional sub-manifolds of the Euclidean space. We also show experimental results including applications to classification and semi-supervised learning within the covariate shift framework and demonstrate some encouraging experimental comparisons. We also show how the parameters of our algorithms can be chosen in a completely unsupervised manner.
Graph Laplacians on Singular Manifolds: Toward understanding complex spaces: graph Laplacians on manifolds with singularities and boundaries
Nov 28, 2012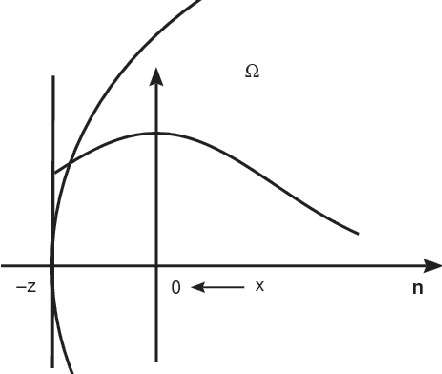
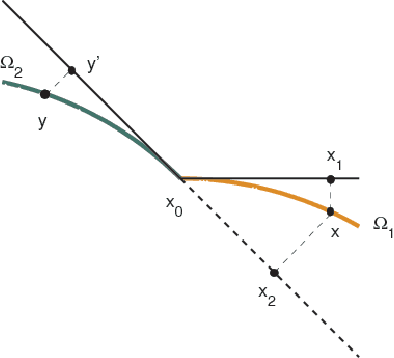
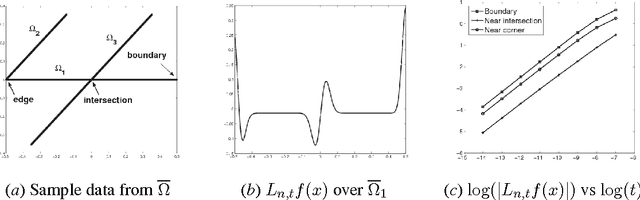
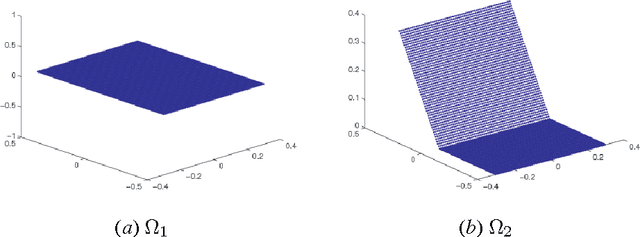
Abstract:Recently, much of the existing work in manifold learning has been done under the assumption that the data is sampled from a manifold without boundaries and singularities or that the functions of interest are evaluated away from such points. At the same time, it can be argued that singularities and boundaries are an important aspect of the geometry of realistic data. In this paper we consider the behavior of graph Laplacians at points at or near boundaries and two main types of other singularities: intersections, where different manifolds come together and sharp "edges", where a manifold sharply changes direction. We show that the behavior of graph Laplacian near these singularities is quite different from that in the interior of the manifolds. In fact, a phenomenon somewhat reminiscent of the Gibbs effect in the analysis of Fourier series, can be observed in the behavior of graph Laplacian near such points. Unlike in the interior of the domain, where graph Laplacian converges to the Laplace-Beltrami operator, near singularities graph Laplacian tends to a first-order differential operator, which exhibits different scaling behavior as a function of the kernel width. One important implication is that while points near the singularities occupy only a small part of the total volume, the difference in scaling results in a disproportionately large contribution to the total behavior. Another significant finding is that while the scaling behavior of the operator is the same near different types of singularities, they are very distinct at a more refined level of analysis. We believe that a comprehensive understanding of these structures in addition to the standard case of a smooth manifold can take us a long way toward better methods for analysis of complex non-linear data and can lead to significant progress in algorithm design.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge