Qianru Wei
DGP-Net: Dense Graph Prototype Network for Few-Shot SAR Target Recognition
Feb 19, 2023



Abstract:The inevitable feature deviation of synthetic aperture radar (SAR) image due to the special imaging principle (depression angle variation) leads to poor recognition accuracy, especially in few-shot learning (FSL). To deal with this problem, we propose a dense graph prototype network (DGP-Net) to eliminate the feature deviation by learning potential features, and classify by learning feature distribution. The role of the prototype in this model is to solve the problem of large distance between congeneric samples taken due to the contingency of single sampling in FSL, and enhance the robustness of the model. Experimental results on the MSTAR dataset show that the DGP-Net has good classification results for SAR images with different depression angles and the recognition accuracy of it is higher than typical FSL methods.
Robust Blind Source Separation by Soft Decision-Directed Non-Unitary Joint Diagonalization
Jun 28, 2021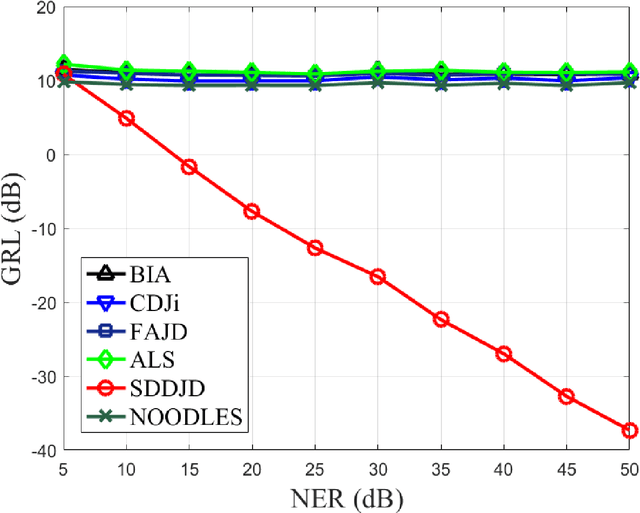
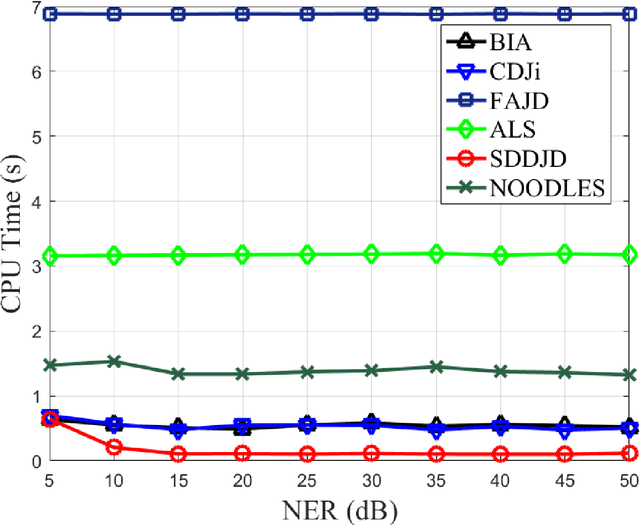
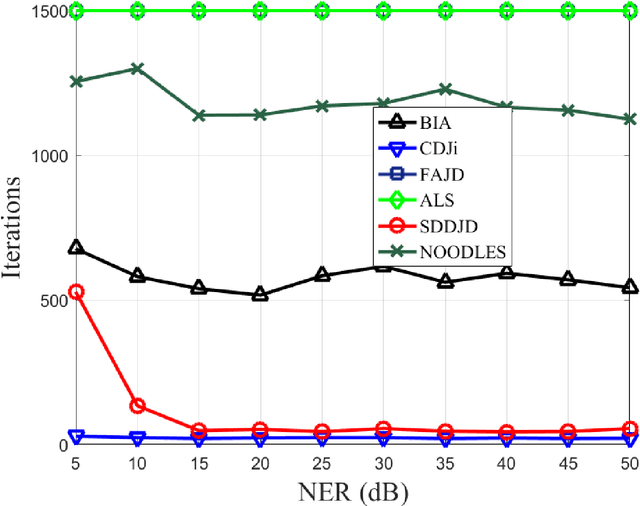
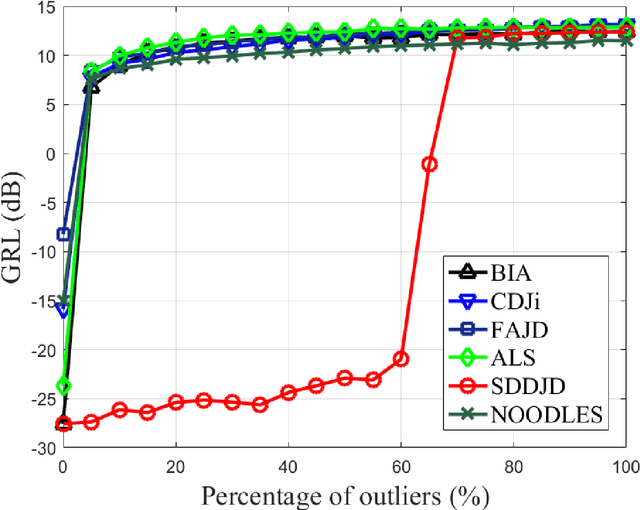
Abstract:Approximate joint diagonalization of a set of matrices provides a powerful framework for numerous statistical signal processing applications. For non-unitary joint diagonalization (NUJD) based on the least-squares (LS) criterion, outliers, also referred to as anomaly or discordant observations, have a negative influence on the performance, since squaring the residuals magnifies the effects of them. To solve this problem, we propose a novel cost function that incorporates the soft decision-directed scheme into the least-squares algorithm and develops an efficient algorithm. The influence of the outliers is mitigated by applying decision-directed weights which are associated with the residual error at each iterative step. Specifically, the mixing matrix is estimated by a modified stationary point method, in which the updating direction is determined based on the linear approximation to the gradient function. Simulation results demonstrate that the proposed algorithm outperforms conventional non-unitary diagonalization algorithms in terms of both convergence performance and robustness to outliers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge