Priya Mani
Hub-VAE: Unsupervised Hub-based Regularization of Variational Autoencoders
Nov 18, 2022Abstract:Exemplar-based methods rely on informative data points or prototypes to guide the optimization of learning algorithms. Such data facilitate interpretable model design and prediction. Of particular interest is the utility of exemplars in learning unsupervised deep representations. In this paper, we leverage hubs, which emerge as frequent neighbors in high-dimensional spaces, as exemplars to regularize a variational autoencoder and to learn a discriminative embedding for unsupervised down-stream tasks. We propose an unsupervised, data-driven regularization of the latent space with a mixture of hub-based priors and a hub-based contrastive loss. Experimental evaluation shows that our algorithm achieves superior cluster separability in the embedding space, and accurate data reconstruction and generation, compared to baselines and state-of-the-art techniques.
Unsupervised Selective Manifold Regularized Matrix Factorization
Oct 20, 2020
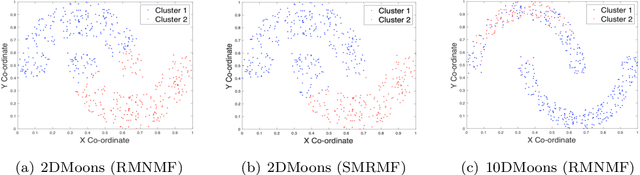

Abstract:Manifold regularization methods for matrix factorization rely on the cluster assumption, whereby the neighborhood structure of data in the input space is preserved in the factorization space. We argue that using the k-neighborhoods of all data points as regularization constraints can negatively affect the quality of the factorization, and propose an unsupervised and selective regularized matrix factorization algorithm to tackle this problem. Our approach jointly learns a sparse set of representatives and their neighbor affinities, and the data factorization. We further propose a fast approximation of our approach by relaxing the selectivity constraints on the data. Our proposed algorithms are competitive against baselines and state-of-the-art manifold regularization and clustering algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge