Unsupervised Selective Manifold Regularized Matrix Factorization
Paper and Code
Oct 20, 2020
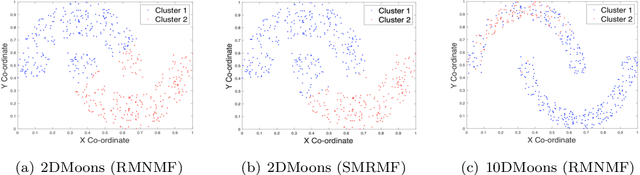

Manifold regularization methods for matrix factorization rely on the cluster assumption, whereby the neighborhood structure of data in the input space is preserved in the factorization space. We argue that using the k-neighborhoods of all data points as regularization constraints can negatively affect the quality of the factorization, and propose an unsupervised and selective regularized matrix factorization algorithm to tackle this problem. Our approach jointly learns a sparse set of representatives and their neighbor affinities, and the data factorization. We further propose a fast approximation of our approach by relaxing the selectivity constraints on the data. Our proposed algorithms are competitive against baselines and state-of-the-art manifold regularization and clustering algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge