The Power of Nudging: Exploring Three Interventions for Metacognitive Skills Instruction across Intelligent Tutoring Systems

Deductive domains are typical of many cognitive skills in that no single problem-solving strategy is always optimal for solving all problems. It was shown that students who know how and when to use each strategy (StrTime) outperformed those who know neither and stick to the default strategy (Default). In this work, students were trained on a logic tutor that supports a default forward-chaining and a backward-chaining (BC) strategy, then a probability tutor that only supports BC. We investigated three types of interventions on teaching the Default students how and when to use which strategy on the logic tutor: Example, Nudge and Presented. Meanwhile, StrTime students received no interventions. Overall, our results show that Nudge outperformed their Default peers and caught up with StrTime on both tutors.

Investigating the Impact of Backward Strategy Learning in a Logic Tutor: Aiding Subgoal Learning towards Improved Problem Solving

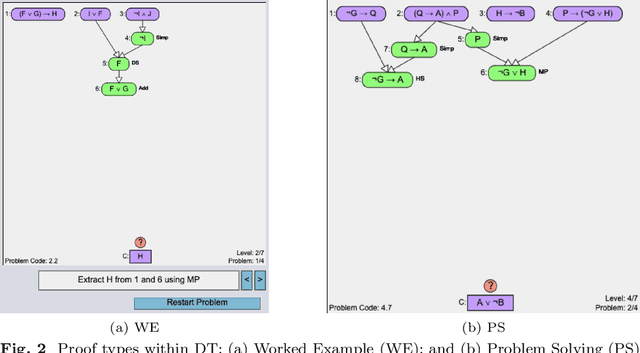
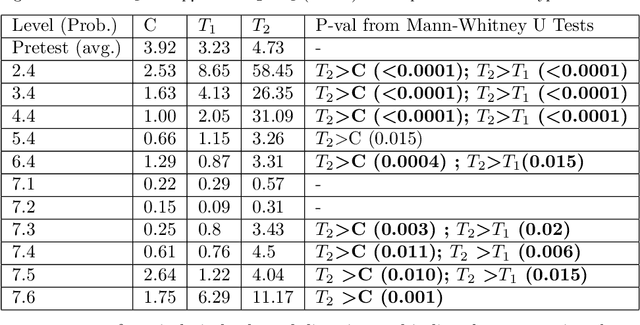
Learning to derive subgoals reduces the gap between experts and students and makes students prepared for future problem solving. Researchers have explored subgoal labeled instructional materials with explanations in traditional problem solving and within tutoring systems to help novices learn to subgoal. However, only a little research is found on problem-solving strategies in relationship with subgoal learning. Also, these strategies are under-explored within computer-based tutors and learning environments. Backward problem-solving strategy is closely related to the process of subgoaling, where problem solving iteratively refines the goal into a new subgoal to reduce difficulty. In this paper, we explore a training strategy for backward strategy learning within an intelligent logic tutor that teaches logic proof construction. The training session involved backward worked examples (BWE) and problem-solving (BPS) to help students learn backward strategy towards improving their subgoaling and problem-solving skills. To evaluate the training strategy, we analyzed students' 1) experience with and engagement in learning backward strategy, 2) performance, and 3) proof construction approaches in new problems that they solved independently without tutor help after each level of training and in post-test. Our results showed that, when new problems were given to solve without any tutor help, students who were trained with both BWE and BPS outperformed students who received none of the treatment or only BWE during training. Additionally, students trained with both BWE and BPS derived subgoals during proof construction with significantly higher efficiency than the other two groups.