Flexible Heteroscedastic Count Regression with Deep Double Poisson Networks

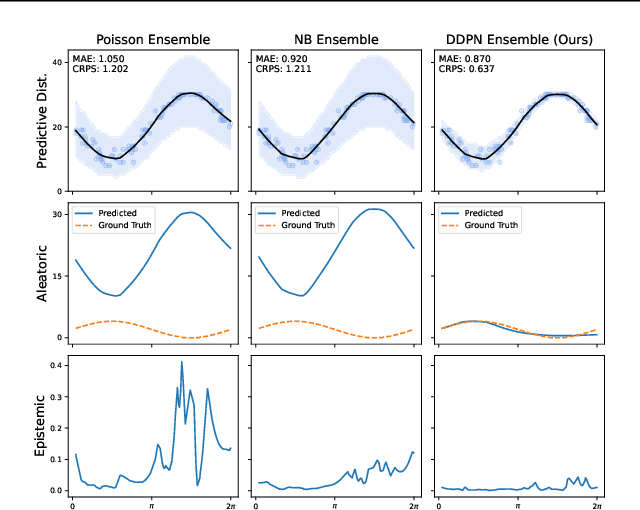
Neural networks that can produce accurate, input-conditional uncertainty representations are critical for real-world applications. Recent progress on heteroscedastic continuous regression has shown great promise for calibrated uncertainty quantification on complex tasks, like image regression. However, when these methods are applied to discrete regression tasks, such as crowd counting, ratings prediction, or inventory estimation, they tend to produce predictive distributions with numerous pathologies. We propose to address these issues by training a neural network to output the parameters of a Double Poisson distribution, which we call the Deep Double Poisson Network (DDPN). In contrast to existing methods that are trained to minimize Gaussian negative log likelihood (NLL), DDPNs produce a proper probability mass function over discrete output. Additionally, DDPNs naturally model under-, over-, and equi-dispersion, unlike networks trained with the more rigid Poisson and Negative Binomial parameterizations. We show DDPNs 1) vastly outperform existing discrete models; 2) meet or exceed the accuracy and flexibility of networks trained with Gaussian NLL; 3) produce proper predictive distributions over discrete counts; and 4) exhibit superior out-of-distribution detection. DDPNs can easily be applied to a variety of count regression datasets including tabular, image, point cloud, and text data.

Personalized Product Assortment with Real-time 3D Perception and Bayesian Payoff Estimation

Product assortment selection is a critical challenge facing physical retailers. Effectively aligning inventory with the preferences of shoppers can increase sales and decrease out-of-stocks. However, in real-world settings the problem is challenging due to the combinatorial explosion of product assortment possibilities. Consumer preferences are typically heterogeneous across space and time, making inventory-preference alignment challenging. Additionally, existing strategies rely on syndicated data, which tends to be aggregated, low resolution, and suffer from high latency. To solve these challenges we introduce a real-time recommendation system, which we call \ours. Our system utilizes recent advances in 3D computer vision for perception and automatic, fine grained sales estimation. These perceptual components run on the edge of the network and facilitate real-time reward signals. Additionally, we develop a Bayesian payoff model to account for noisy estimates from 3D LIDAR data. We rely on spatial clustering to allow the system to adapt to heterogeneous consumer preferences, and a graph-based candidate generation algorithm to address the combinatorial search problem. We test our system in real-world stores across two, 6-8 week A/B tests with beverage products and demonstrate a 35% and 27\% increase in sales respectively. Finally, we monitor the deployed system for a period of 28 weeks with an observational study and show a 9.4\% increase in sales.

On Measuring Calibration of Discrete Probabilistic Neural Networks

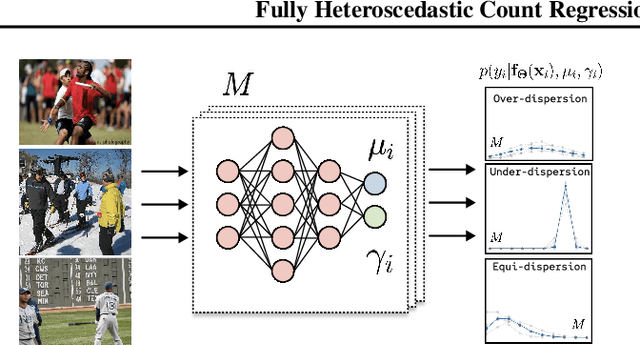
As machine learning systems become increasingly integrated into real-world applications, accurately representing uncertainty is crucial for enhancing their safety, robustness, and reliability. Training neural networks to fit high-dimensional probability distributions via maximum likelihood has become an effective method for uncertainty quantification. However, such models often exhibit poor calibration, leading to overconfident predictions. Traditional metrics like Expected Calibration Error (ECE) and Negative Log Likelihood (NLL) have limitations, including biases and parametric assumptions. This paper proposes a new approach using conditional kernel mean embeddings to measure calibration discrepancies without these biases and assumptions. Preliminary experiments on synthetic data demonstrate the method's potential, with future work planned for more complex applications.

Probabilistic Offline Policy Ranking with Approximate Bayesian Computation

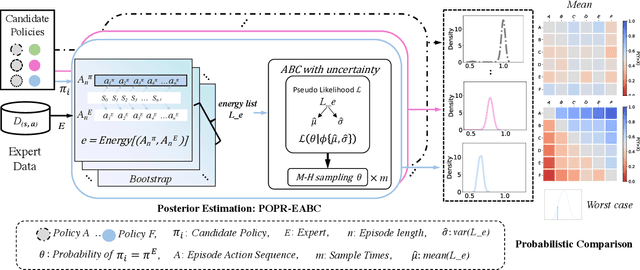
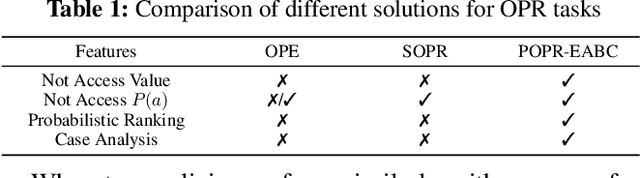
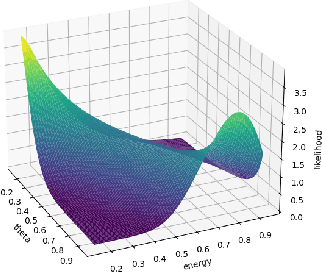
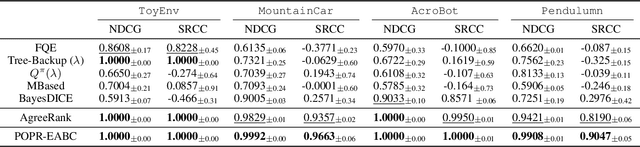
In practice, it is essential to compare and rank candidate policies offline before real-world deployment for safety and reliability. Prior work seeks to solve this offline policy ranking (OPR) problem through value-based methods, such as Off-policy evaluation (OPE). However, they fail to analyze special cases performance (e.g., worst or best cases), due to the lack of holistic characterization of policies performance. It is even more difficult to estimate precise policy values when the reward is not fully accessible under sparse settings. In this paper, we present Probabilistic Offline Policy Ranking (POPR), a framework to address OPR problems by leveraging expert data to characterize the probability of a candidate policy behaving like experts, and approximating its entire performance posterior distribution to help with ranking. POPR does not rely on value estimation, and the derived performance posterior can be used to distinguish candidates in worst, best, and average-cases. To estimate the posterior, we propose POPR-EABC, an Energy-based Approximate Bayesian Computation (ABC) method conducting likelihood-free inference. POPR-EABC reduces the heuristic nature of ABC by a smooth energy function, and improves the sampling efficiency by a pseudo-likelihood. We empirically demonstrate that POPR-EABC is adequate for evaluating policies in both discrete and continuous action spaces across various experiment environments, and facilitates probabilistic comparisons of candidate policies before deployment.

A Probabilistic Simulator of Spatial Demand for Product Allocation

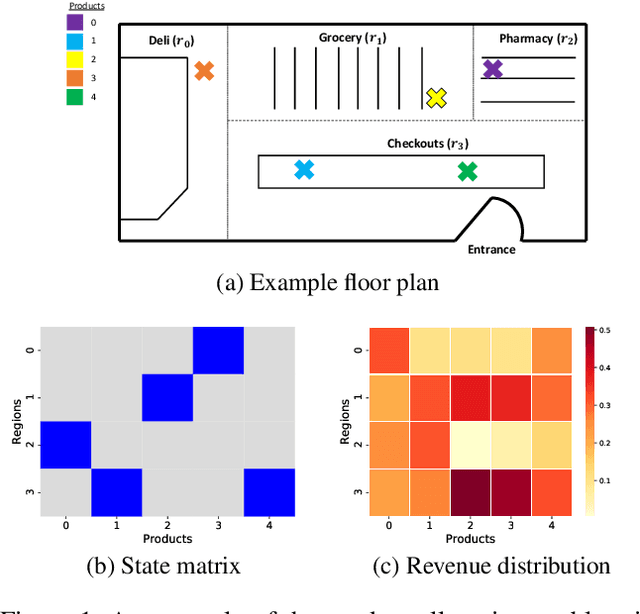
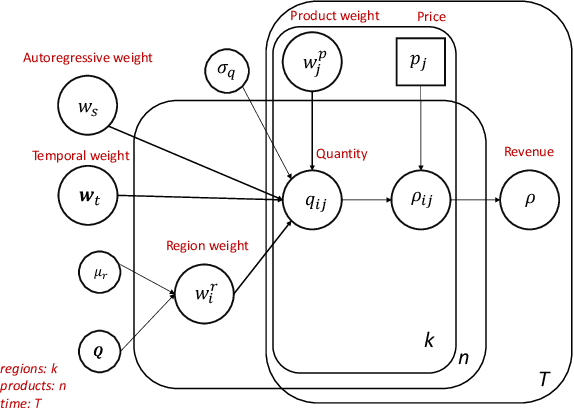
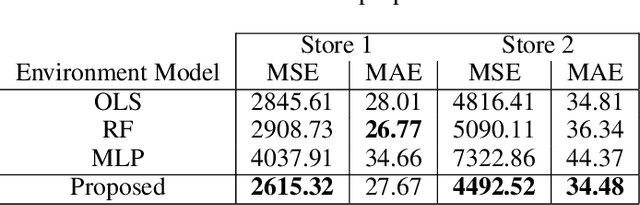
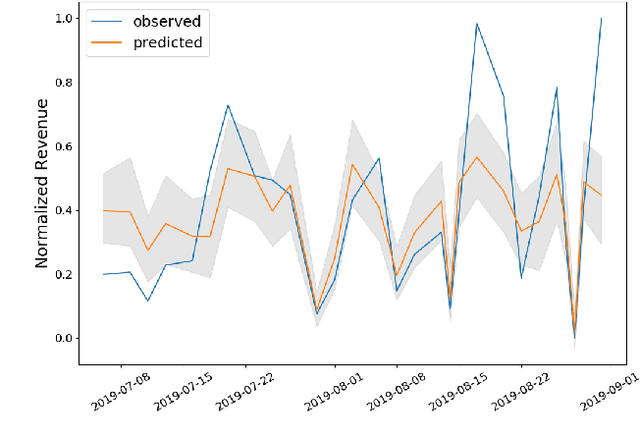
Connecting consumers with relevant products is a very important problem in both online and offline commerce. In physical retail, product placement is an effective way to connect consumers with products. However, selecting product locations within a store can be a tedious process. Moreover, learning important spatial patterns in offline retail is challenging due to the scarcity of data and the high cost of exploration and experimentation in the physical world. To address these challenges, we propose a stochastic model of spatial demand in physical retail. We show that the proposed model is more predictive of demand than existing baselines. We also perform a preliminary study into different automation techniques and show that an optimal product allocation policy can be learned through Deep Q-Learning.