Adaptation of uncertainty-penalized Bayesian information criterion for parametric partial differential equation discovery

Data-driven discovery of partial differential equations (PDEs) has emerged as a promising approach for deriving governing physics when domain knowledge about observed data is limited. Despite recent progress, the identification of governing equations and their parametric dependencies using conventional information criteria remains challenging in noisy situations, as the criteria tend to select overly complex PDEs. In this paper, we introduce an extension of the uncertainty-penalized Bayesian information criterion (UBIC), which is adapted to solve parametric PDE discovery problems efficiently without requiring computationally expensive PDE simulations. This extended UBIC uses quantified PDE uncertainty over different temporal or spatial points to prevent overfitting in model selection. The UBIC is computed with data transformation based on power spectral densities to discover the governing parametric PDE that truly captures qualitative features in frequency space with a few significant terms and their parametric dependencies (i.e., the varying PDE coefficients), evaluated with confidence intervals. Numerical experiments on canonical PDEs demonstrate that our extended UBIC can identify the true number of terms and their varying coefficients accurately, even in the presence of noise. The code is available at \url{https://github.com/Pongpisit-Thanasutives/parametric-discovery}.

On uncertainty-penalized Bayesian information criterion

The uncertainty-penalized information criterion (UBIC) has been proposed as a new model-selection criterion for data-driven partial differential equation (PDE) discovery. In this paper, we show that using the UBIC is equivalent to employing the conventional BIC to a set of overparameterized models derived from the potential regression models of different complexity measures. The result indicates that the asymptotic property of the UBIC and BIC holds indifferently.

Adaptive Uncertainty-Guided Model Selection for Data-Driven PDE Discovery

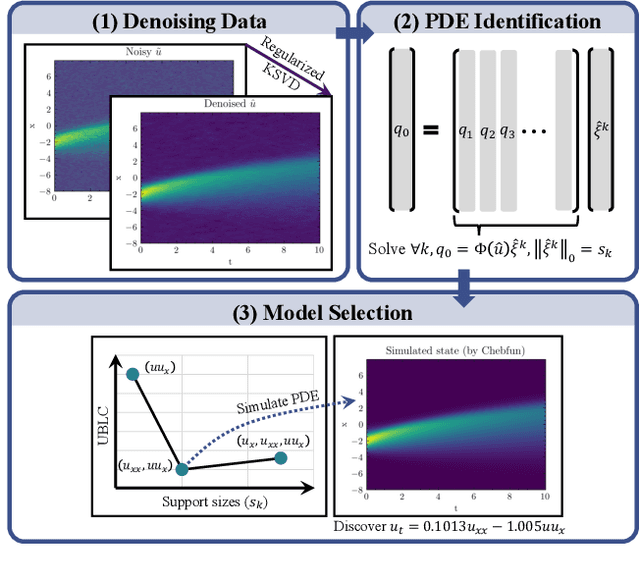
We propose a new parameter-adaptive uncertainty-penalized Bayesian information criterion (UBIC) to prioritize the parsimonious partial differential equation (PDE) that sufficiently governs noisy spatial-temporal observed data with few reliable terms. Since the naive use of the BIC for model selection has been known to yield an undesirable overfitted PDE, the UBIC penalizes the found PDE not only by its complexity but also the quantified uncertainty, derived from the model supports' coefficient of variation in a probabilistic view. We also introduce physics-informed neural network learning as a simulation-based approach to further validate the selected PDE flexibly against the other discovered PDE. Numerical results affirm the successful application of the UBIC in identifying the true governing PDE. Additionally, we reveal an interesting effect of denoising the observed data on improving the trade-off between the BIC score and model complexity. Code is available at https://github.com/Pongpisit-Thanasutives/UBIC.

Noise-aware Physics-informed Machine Learning for Robust PDE Discovery

This work is concerned with discovering the governing partial differential equation (PDE) of a physical system. Existing methods have demonstrated the PDE identification from finite observations but failed to maintain satisfying performance against noisy data, partly owing to suboptimal estimated derivatives and found PDE coefficients. We address the issues by introducing a noise-aware physics-informed machine learning (nPIML) framework to discover the governing PDE from data following arbitrary distributions. Our proposals are twofold. First, we propose a couple of neural networks, namely solver and preselector, which yield an interpretable neural representation of the hidden physical constraint. After they are jointly trained, the solver network approximates potential candidates, e.g., partial derivatives, which are then fed to the sparse regression algorithm that initially unveils the most likely parsimonious PDE, decided according to the information criterion. Second, we propose the denoising physics-informed neural networks (dPINNs), based on Discrete Fourier Transform (DFT), to deliver a set of the optimal finetuned PDE coefficients respecting the noise-reduced variables. The denoising PINNs' structures are compartmentalized into forefront projection networks and a PINN, by which the formerly learned solver initializes. Our extensive experiments on five canonical PDEs affirm that the proposed framework presents a robust and interpretable approach for PDE discovery, applicable to a wide range of systems, possibly complicated by noise.

Adversarial Multi-task Learning Enhanced Physics-informed Neural Networks for Solving Partial Differential Equations

Recently, researchers have utilized neural networks to accurately solve partial differential equations (PDEs), enabling the mesh-free method for scientific computation. Unfortunately, the network performance drops when encountering a high nonlinearity domain. To improve the generalizability, we introduce the novel approach of employing multi-task learning techniques, the uncertainty-weighting loss and the gradients surgery, in the context of learning PDE solutions. The multi-task scheme exploits the benefits of learning shared representations, controlled by cross-stitch modules, between multiple related PDEs, which are obtainable by varying the PDE parameterization coefficients, to generalize better on the original PDE. Encouraging the network pay closer attention to the high nonlinearity domain regions that are more challenging to learn, we also propose adversarial training for generating supplementary high-loss samples, similarly distributed to the original training distribution. In the experiments, our proposed methods are found to be effective and reduce the error on the unseen data points as compared to the previous approaches in various PDE examples, including high-dimensional stochastic PDEs.

Encoder-Decoder Based Convolutional Neural Networks with Multi-Scale-Aware Modules for Crowd Counting

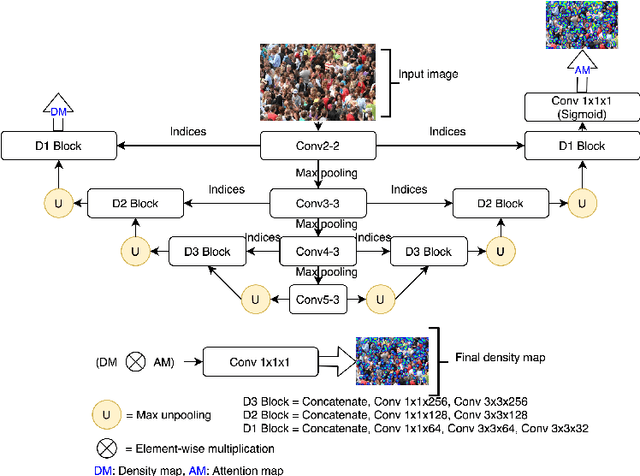
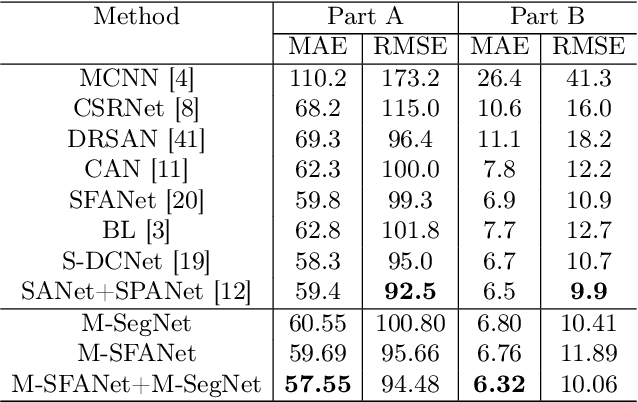
In this paper, we proposed two modified neural network architectures based on SFANet and SegNet respectively for accurate and efficient crowd counting. Inspired by SFANet, the first model is attached with two novel multi-scale-aware modules, called ASSP and CAN. This model is named M-SFANet. The encoder of M-SFANet is enhanced with ASSP containing parallel atrous convolutional layers with different sampling rates and hence able to extract multi-scale features of the target object and incorporate larger context. To further deal with scale variation throughout an input image, we leverage contextual module called CAN which adaptively encodes the scales of the contextual information. The combination yields an effective model for counting in both dense and sparse crowd scenes. Based on SFANet decoder structure, M-SFANet's decoder has dual paths, for density map generation and attention map generation. The second model is called M-SegNet, which is produced by replacing the bilinear upsampling in SFANet with max unpooling that is used in SegNet. This change provides the faster model while providing competitive counting performance. Designed for high-speed surveillance applications, M-SegNet has no additional multi-scale-aware module in order to not increase the complexity. Both models are encoder-decoder based architectures and are end-to-end trainable. We also conduct extensive experiments on five crowd counting datasets and one vehicle counting dataset to show that these modifications yield algorithms that could outperform some of state-of-the-art crowd counting methods. Codes are available at https://github.com/Pongpisit-Thanasutives/Variations-of-SFANet-for-Crowd-Counting.