Piotr Kozlowski
Multifrequency 3D Elasticity Reconstruction withStructured Sparsity and ADMM
Nov 23, 2021
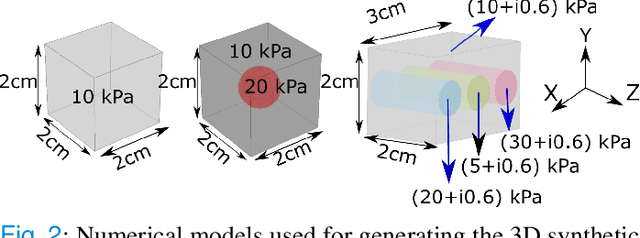


Abstract:We introduce a model-based iterative method to obtain shear modulus images of tissue using magnetic resonance elastography. The method jointly finds the displacement field that best fits multifrequency tissue displacement data and the corresponding shear modulus. The displacement satisfies a viscoelastic wave equation constraint, discretized using the finite element method. Sparsifying regularization terms in both shear modulus and the displacement are used in the cost function minimized for the best fit. The formulated problem is bi-convex. Its solution can be obtained iteratively by using the alternating direction method of multipliers. Sparsifying regularizations and the wave equation constraint filter out sensor noise and compressional waves. Our method does not require bandpass filtering as a preprocessing step and converges fast irrespective of the initialization. We evaluate our new method in multiple in silico and phantom experiments, with comparisons with existing methods, and we show improvements in contrast to noise and signal to noise ratios. Results from an in vivo liver imaging study show elastograms with mean elasticity comparable to other values reported in the literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge