Philipp Joppich
Classification and Uncertainty Quantification of Corrupted Data using Semi-Supervised Autoencoders
May 27, 2021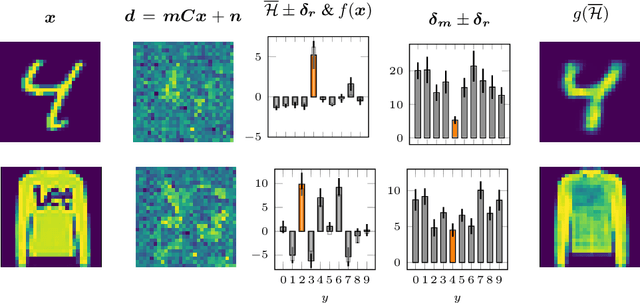
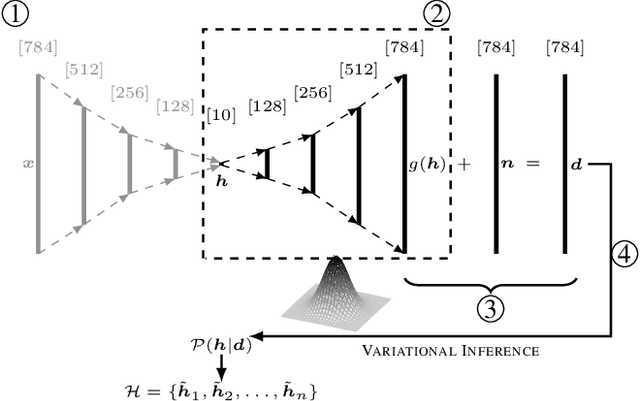
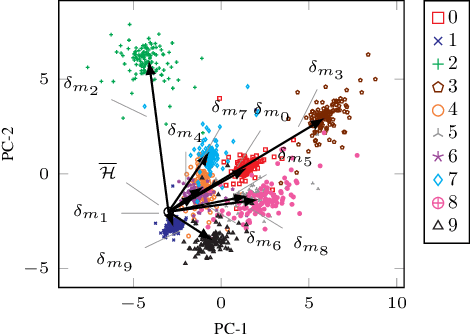
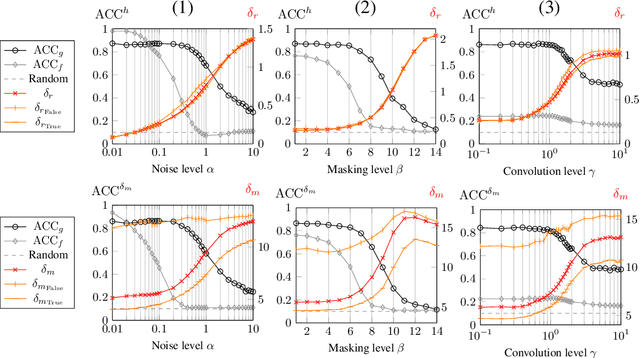
Abstract:Parametric and non-parametric classifiers often have to deal with real-world data, where corruptions like noise, occlusions, and blur are unavoidable - posing significant challenges. We present a probabilistic approach to classify strongly corrupted data and quantify uncertainty, despite the model only having been trained with uncorrupted data. A semi-supervised autoencoder trained on uncorrupted data is the underlying architecture. We use the decoding part as a generative model for realistic data and extend it by convolutions, masking, and additive Gaussian noise to describe imperfections. This constitutes a statistical inference task in terms of the optimal latent space activations of the underlying uncorrupted datum. We solve this problem approximately with Metric Gaussian Variational Inference (MGVI). The supervision of the autoencoder's latent space allows us to classify corrupted data directly under uncertainty with the statistically inferred latent space activations. Furthermore, we demonstrate that the model uncertainty strongly depends on whether the classification is correct or wrong, setting a basis for a statistical "lie detector" of the classification. Independent of that, we show that the generative model can optimally restore the uncorrupted datum by decoding the inferred latent space activations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge