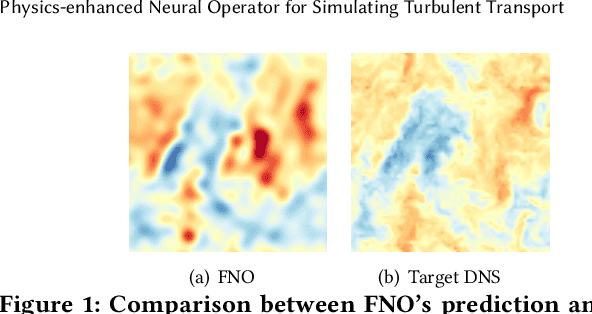
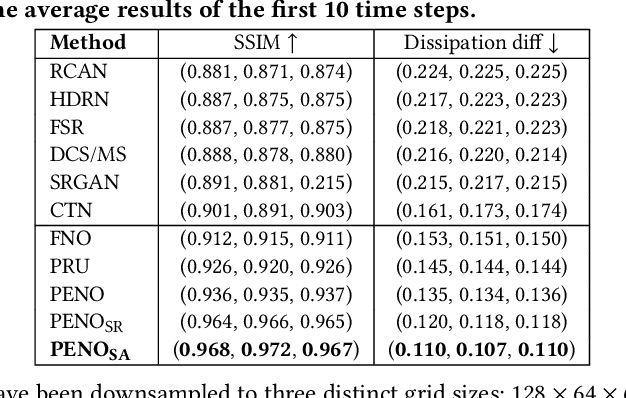
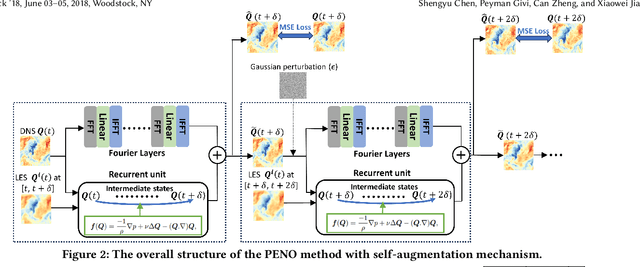
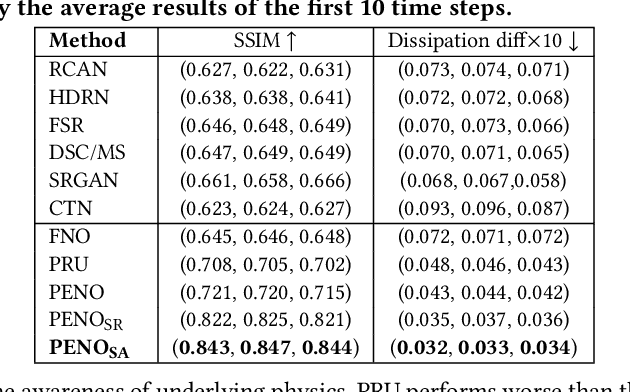
Physics-enhanced Neural Operator for Simulating Turbulent Transport

The precise simulation of turbulent flows is of immense importance in a variety of scientific and engineering fields, including climate science, freshwater science, and the development of energy-efficient manufacturing processes. Within the realm of turbulent flow simulation, direct numerical simulation (DNS) is widely considered to be the most reliable approach, but it is prohibitively expensive for long-term simulation at fine spatial scales. Given the pressing need for efficient simulation, there is an increasing interest in building machine learning models for turbulence, either by reconstructing DNS from alternative low-fidelity simulations or by predicting DNS based on the patterns learned from historical data. However, standard machine learning techniques remain limited in capturing complex spatio-temporal characteristics of turbulent flows, resulting in limited performance and generalizability. This paper presents a novel physics-enhanced neural operator (PENO) that incorporates physical knowledge of partial differential equations (PDEs) to accurately model flow dynamics. The model is further refined by a self-augmentation mechanism to reduce the accumulated error in long-term simulations. The proposed method is evaluated through its performance on two distinct sets of 3D turbulent flow data, showcasing the model's capability to reconstruct high-resolution DNS data, maintain the inherent physical properties of flow transport, and generate flow simulations across various resolutions. Additionally, experimental results on multiple 2D vorticity flow series, generated by different PDEs, highlight the transferability and generalizability of the proposed method. This confirms its applicability to a wide range of real-world scenarios in which extensive simulations are needed under diverse settings.

Reconstructing Turbulent Flows Using Physics-Aware Spatio-Temporal Dynamics and Test-Time Refinement

Simulating turbulence is critical for many societally important applications in aerospace engineering, environmental science, the energy industry, and biomedicine. Large eddy simulation (LES) has been widely used as an alternative to direct numerical simulation (DNS) for simulating turbulent flows due to its reduced computational cost. However, LES is unable to capture all of the scales of turbulent transport accurately. Reconstructing DNS from low-resolution LES is critical for many scientific and engineering disciplines, but it poses many challenges to existing super-resolution methods due to the spatio-temporal complexity of turbulent flows. In this work, we propose a new physics-guided neural network for reconstructing the sequential DNS from low-resolution LES data. The proposed method leverages the partial differential equation that underlies the flow dynamics in the design of spatio-temporal model architecture. A degradation-based refinement method is also developed to enforce physical constraints and further reduce the accumulated reconstruction errors over long periods. The results on two different types of turbulent flow data confirm the superiority of the proposed method in reconstructing the high-resolution DNS data and preserving the physical characteristics of flow transport.

Reconstructing High-resolution Turbulent Flows Using Physics-Guided Neural Networks

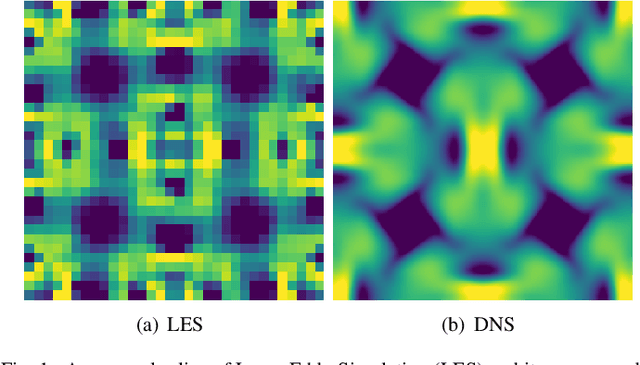
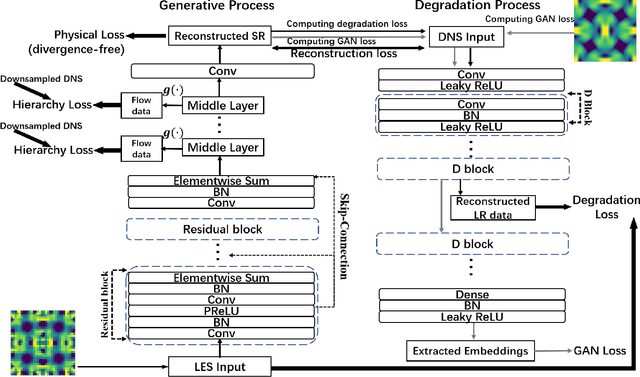
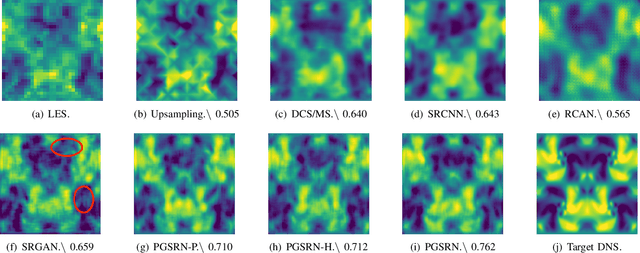
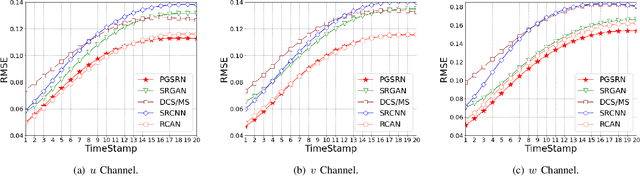
Direct numerical simulation (DNS) of turbulent flows is computationally expensive and cannot be applied to flows with large Reynolds numbers. Large eddy simulation (LES) is an alternative that is computationally less demanding, but is unable to capture all of the scales of turbulent transport accurately. Our goal in this work is to build a new data-driven methodology based on super-resolution techniques to reconstruct DNS data from LES predictions. We leverage the underlying physical relationships to regularize the relationships amongst different physical variables. We also introduce a hierarchical generative process and a reverse degradation process to fully explore the correspondence between DNS and LES data. We demonstrate the effectiveness of our method through a single-snapshot experiment and a cross-time experiment. The results confirm that our method can better reconstruct high-resolution DNS data over space and over time in terms of pixel-wise reconstruction error and structural similarity. Visual comparisons show that our method performs much better in capturing fine-level flow dynamics.