Making Decisions Using Sets of Probabilities: Updating, Time Consistency, and Calibration

We consider how an agent should update her beliefs when her beliefs are represented by a set P of probability distributions, given that the agent makes decisions using the minimax criterion, perhaps the best-studied and most commonly-used criterion in the literature. We adopt a game-theoretic framework, where the agent plays against a bookie, who chooses some distribution from P. We consider two reasonable games that differ in what the bookie knows when he makes his choice. Anomalies that have been observed before, like time inconsistency, can be understood as arising because different games are being played, against bookies with different information. We characterize the important special cases in which the optimal decision rules according to the minimax criterion amount to either conditioning or simply ignoring the information. Finally, we consider the relationship between updating and calibration when uncertainty is described by sets of probabilities. Our results emphasize the key role of the rectangularity condition of Epstein and Schneider.

Minimum Encoding Approaches for Predictive Modeling

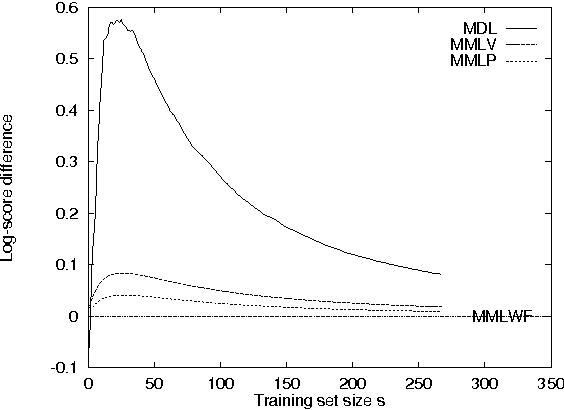
We analyze differences between two information-theoretically motivated approaches to statistical inference and model selection: the Minimum Description Length (MDL) principle, and the Minimum Message Length (MML) principle. Based on this analysis, we present two revised versions of MML: a pointwise estimator which gives the MML-optimal single parameter model, and a volumewise estimator which gives the MML-optimal region in the parameter space. Our empirical results suggest that with small data sets, the MDL approach yields more accurate predictions than the MML estimators. The empirical results also demonstrate that the revised MML estimators introduced here perform better than the original MML estimator suggested by Wallace and Freeman.