Minimum Encoding Approaches for Predictive Modeling

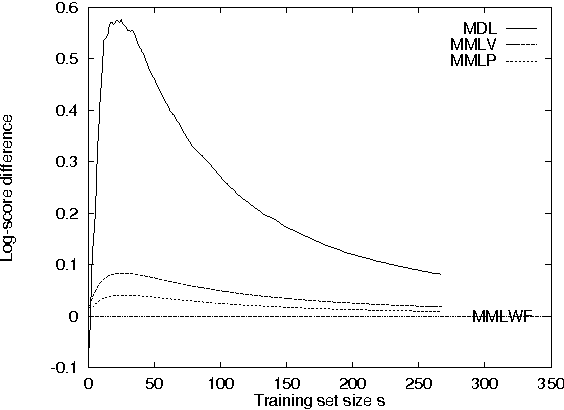
We analyze differences between two information-theoretically motivated approaches to statistical inference and model selection: the Minimum Description Length (MDL) principle, and the Minimum Message Length (MML) principle. Based on this analysis, we present two revised versions of MML: a pointwise estimator which gives the MML-optimal single parameter model, and a volumewise estimator which gives the MML-optimal region in the parameter space. Our empirical results suggest that with small data sets, the MDL approach yields more accurate predictions than the MML estimators. The empirical results also demonstrate that the revised MML estimators introduced here perform better than the original MML estimator suggested by Wallace and Freeman.

On Supervised Selection of Bayesian Networks

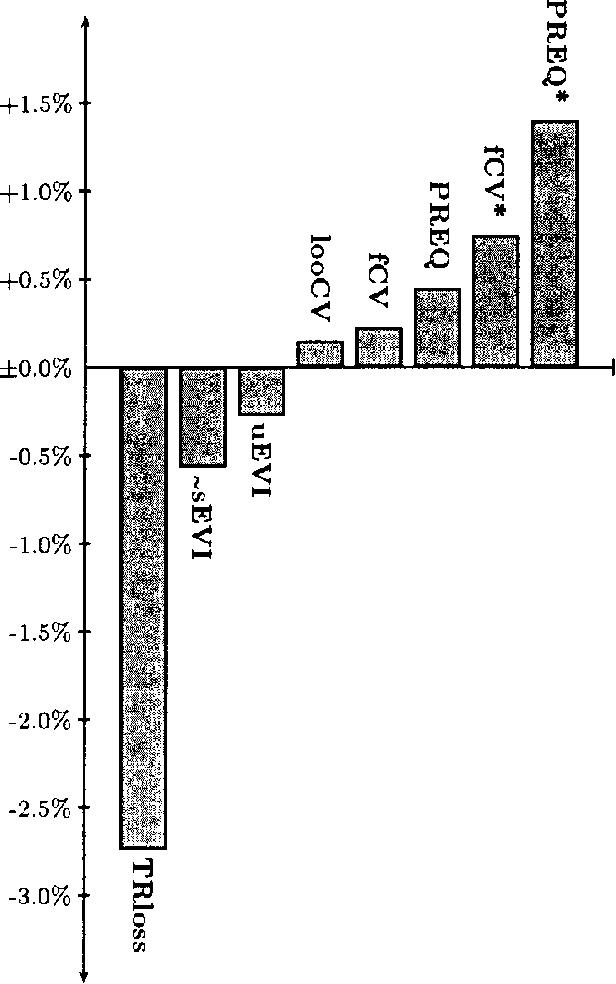
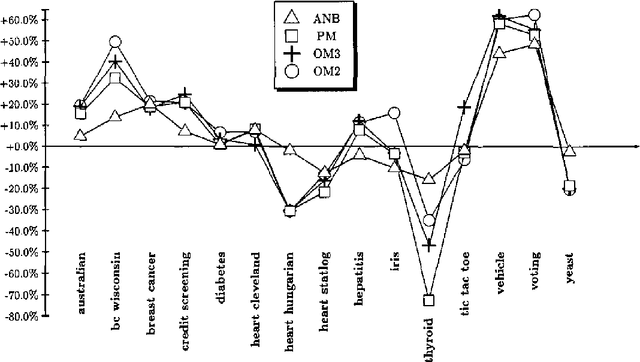
Given a set of possible models (e.g., Bayesian network structures) and a data sample, in the unsupervised model selection problem the task is to choose the most accurate model with respect to the domain joint probability distribution. In contrast to this, in supervised model selection it is a priori known that the chosen model will be used in the future for prediction tasks involving more ``focused' predictive distributions. Although focused predictive distributions can be produced from the joint probability distribution by marginalization, in practice the best model in the unsupervised sense does not necessarily perform well in supervised domains. In particular, the standard marginal likelihood score is a criterion for the unsupervised task, and, although frequently used for supervised model selection also, does not perform well in such tasks. In this paper we study the performance of the marginal likelihood score empirically in supervised Bayesian network selection tasks by using a large number of publicly available classification data sets, and compare the results to those obtained by alternative model selection criteria, including empirical crossvalidation methods, an approximation of a supervised marginal likelihood measure, and a supervised version of Dawids prequential(predictive sequential) principle.The results demonstrate that the marginal likelihood score does NOT perform well FOR supervised model selection, WHILE the best results are obtained BY using Dawids prequential r napproach.

Classifier Learning with Supervised Marginal Likelihood

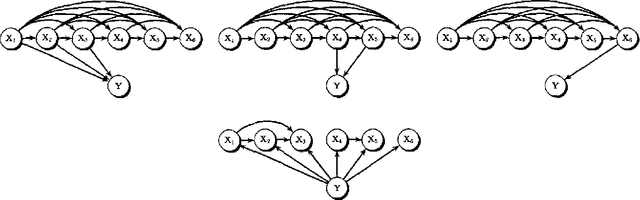
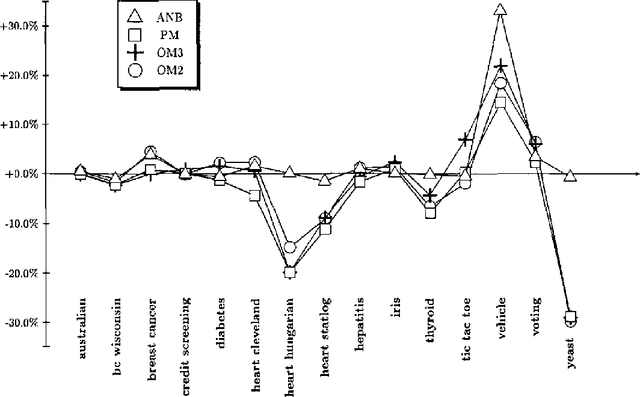
It has been argued that in supervised classification tasks, in practice it may be more sensible to perform model selection with respect to some more focused model selection score, like the supervised (conditional) marginal likelihood, than with respect to the standard marginal likelihood criterion. However, for most Bayesian network models, computing the supervised marginal likelihood score takes exponential time with respect to the amount of observed data. In this paper, we consider diagnostic Bayesian network classifiers where the significant model parameters represent conditional distributions for the class variable, given the values of the predictor variables, in which case the supervised marginal likelihood can be computed in linear time with respect to the data. As the number of model parameters grows in this case exponentially with respect to the number of predictors, we focus on simple diagnostic models where the number of relevant predictors is small, and suggest two approaches for applying this type of models in classification. The first approach is based on mixtures of simple diagnostic models, while in the second approach we apply the small predictor sets of the simple diagnostic models for augmenting the Naive Bayes classifier.

On Sensitivity of the MAP Bayesian Network Structure to the Equivalent Sample Size Parameter

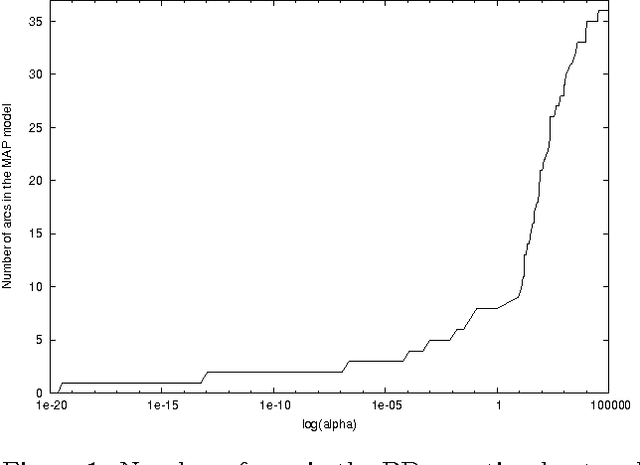
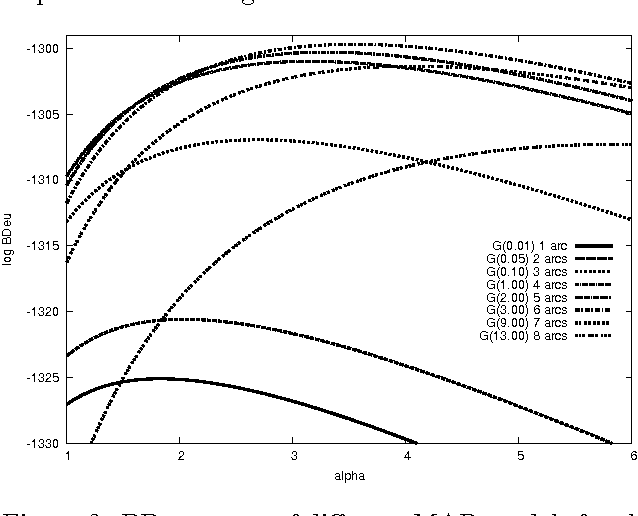
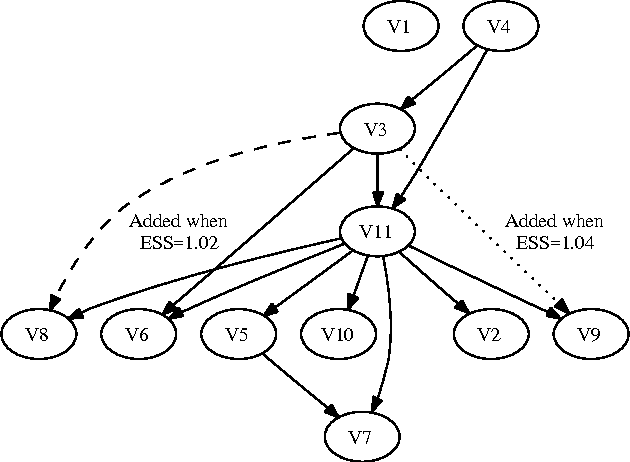
BDeu marginal likelihood score is a popular model selection criterion for selecting a Bayesian network structure based on sample data. This non-informative scoring criterion assigns same score for network structures that encode same independence statements. However, before applying the BDeu score, one must determine a single parameter, the equivalent sample size alpha. Unfortunately no generally accepted rule for determining the alpha parameter has been suggested. This is disturbing, since in this paper we show through a series of concrete experiments that the solution of the network structure optimization problem is highly sensitive to the chosen alpha parameter value. Based on these results, we are able to give explanations for how and why this phenomenon happens, and discuss ideas for solving this problem.