Identifying Heterogeneous Treatment Effects in Multiple Outcomes using Joint Confidence Intervals

Heterogeneous treatment effects (HTEs) are commonly identified during randomized controlled trials (RCTs). Identifying subgroups of patients with similar treatment effects is of high interest in clinical research to advance precision medicine. Often, multiple clinical outcomes are measured during an RCT, each having a potentially heterogeneous effect. Recently there has been high interest in identifying subgroups from HTEs, however, there has been less focus on developing tools in settings where there are multiple outcomes. In this work, we propose a framework for partitioning the covariate space to identify subgroups across multiple outcomes based on the joint CIs. We test our algorithm on synthetic and semi-synthetic data where there are two outcomes, and demonstrate that our algorithm is able to capture the HTE in both outcomes simultaneously.

Discrepancies in Epidemiological Modeling of Aggregated Heterogeneous Data

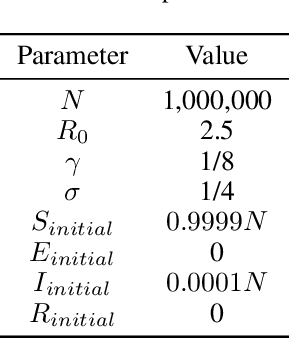
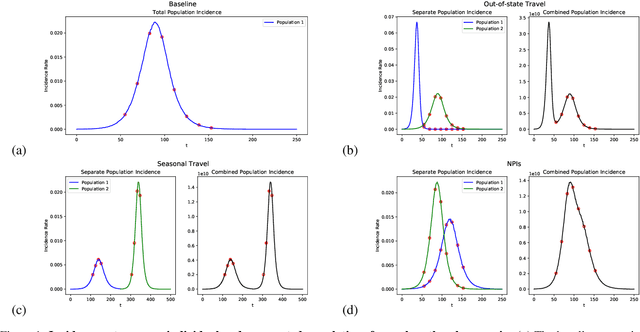
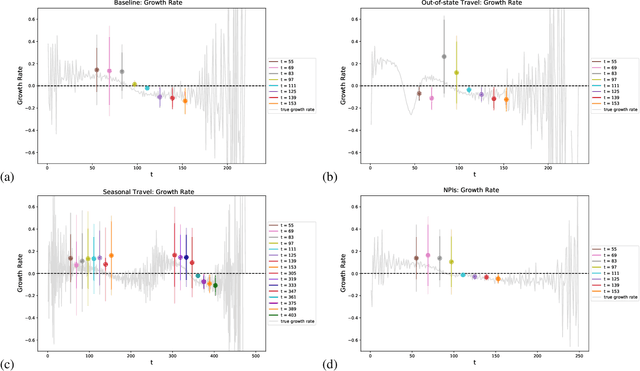
Within epidemiological modeling, the majority of analyses assume a single epidemic process for generating ground-truth data. However, this assumed data generation process can be unrealistic, since data sources for epidemics are often aggregated across geographic regions and communities. As a result, state-of-the-art models for estimating epidemiological parameters, e.g.~transmission rates, can be inappropriate when faced with complex systems. Our work empirically demonstrates some limitations of applying epidemiological models to aggregated datasets. We generate three complex outbreak scenarios by combining incidence curves from multiple epidemics that are independently simulated via SEIR models with different sets of parameters. Using these scenarios, we assess the robustness of a state-of-the-art Bayesian inference method that estimates the epidemic trajectory from viral load surveillance data. We evaluate two data-generating models within this Bayesian inference framework: a simple exponential growth model and a highly flexible Gaussian process prior model. Our results show that both models generate accurate transmission rate estimates for the combined incidence curve at the cost of generating biased estimates for each underlying epidemic, reflecting highly heterogeneous underlying population dynamics. The exponential growth model, while interpretable, is unable to capture the complexity of the underlying epidemics. With sufficient surveillance data, the Gaussian process prior model captures the shape of complex trajectories, but is imprecise for periods of low data coverage. Thus, our results highlight the potential pitfalls of neglecting complexity and heterogeneity in the data generation process, which can mask underlying location- and population-specific epidemic dynamics.