A Tool for Integer Homology Computation: Lambda-At Model

In this paper, we formalize the notion of lambda-AT-model (where $\lambda$ is a non-null integer) for a given chain complex, which allows the computation of homological information in the integer domain avoiding using the Smith Normal Form of the boundary matrices. We present an algorithm for computing such a model, obtaining Betti numbers, the prime numbers p involved in the invariant factors of the torsion subgroup of homology, the amount of invariant factors that are a power of p and a set of representative cycles of generators of homology mod p, for each p. Moreover, we establish the minimum valid lambda for such a construction, what cuts down the computational costs related to the torsion subgroup. The tools described here are useful to determine topological information of nD structured objects such as simplicial, cubical or simploidal complexes and are applicable to extract such an information from digital pictures.

On the Cohomology of 3D Digital Images

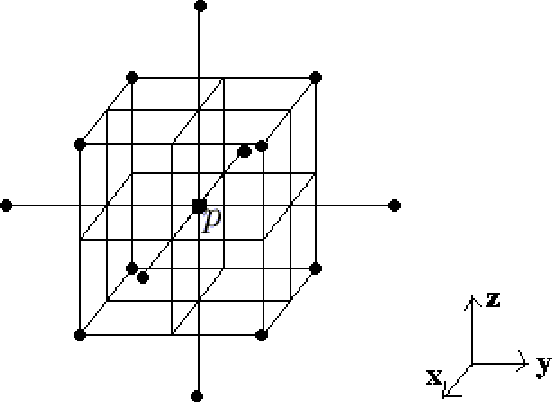
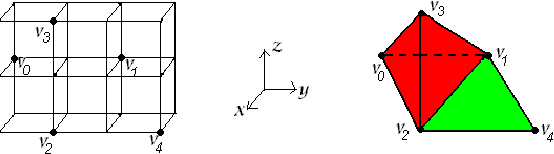
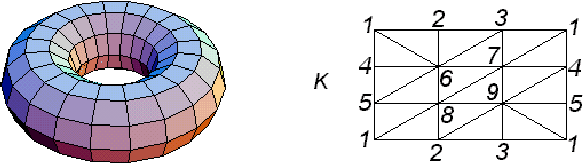
We propose a method for computing the cohomology ring of three--dimensional (3D) digital binary-valued pictures. We obtain the cohomology ring of a 3D digital binary--valued picture $I$, via a simplicial complex K(I)topologically representing (up to isomorphisms of pictures) the picture I. The usefulness of a simplicial description of the "digital" cohomology ring of 3D digital binary-valued pictures is tested by means of a small program visualizing the different steps of the method. Some examples concerning topological thinning, the visualization of representative (co)cycles of (co)homology generators and the computation of the cup product on the cohomology of simple pictures are showed.