On the Cohomology of 3D Digital Images
Paper and Code
May 23, 2011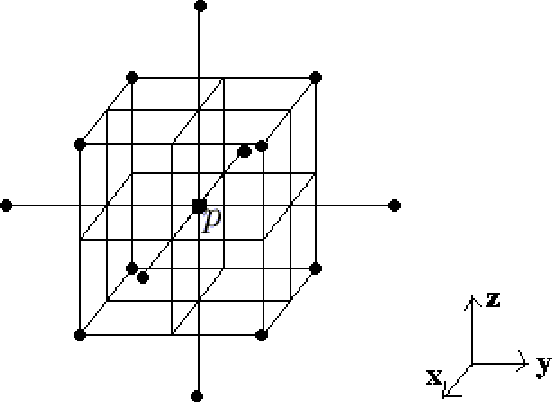
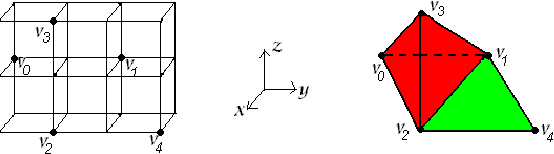
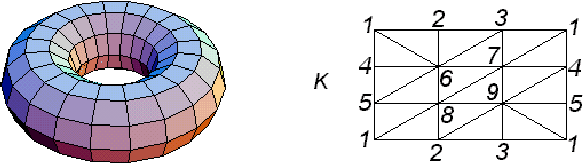

We propose a method for computing the cohomology ring of three--dimensional (3D) digital binary-valued pictures. We obtain the cohomology ring of a 3D digital binary--valued picture $I$, via a simplicial complex K(I)topologically representing (up to isomorphisms of pictures) the picture I. The usefulness of a simplicial description of the "digital" cohomology ring of 3D digital binary-valued pictures is tested by means of a small program visualizing the different steps of the method. Some examples concerning topological thinning, the visualization of representative (co)cycles of (co)homology generators and the computation of the cup product on the cohomology of simple pictures are showed.
* Discrete Applied Mathematics, Volume 147, Issues 2-3, 15 April
2005, Pages 245-263 * Special Issue: Advances in Discrete Geometry and Topology
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge