Pedrito Maynard-Reid II
Miami University
Aggregating Learned Probabilistic Beliefs
Jan 10, 2013


Abstract:We consider the task of aggregating beliefs of severalexperts. We assume that these beliefs are represented as probabilitydistributions. We argue that the evaluation of any aggregationtechnique depends on the semantic context of this task. We propose aframework, in which we assume that nature generates samples from a`true' distribution and different experts form their beliefs based onthe subsets of the data they have a chance to observe. Naturally, theideal aggregate distribution would be the one learned from thecombined sample sets. Such a formulation leads to a natural way tomeasure the accuracy of the aggregation mechanism.We show that the well-known aggregation operator LinOP is ideallysuited for that task. We propose a LinOP-based learning algorithm,inspired by the techniques developed for Bayesian learning, whichaggregates the experts' distributions represented as Bayesiannetworks. Our preliminary experiments show that this algorithmperforms well in practice.
Representing and Aggregating Conflicting Beliefs
Mar 11, 2002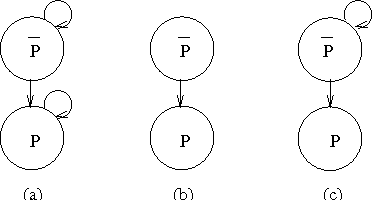
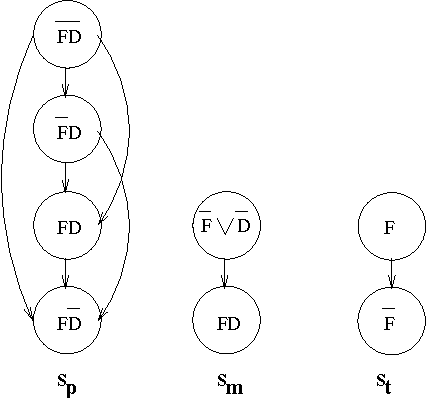
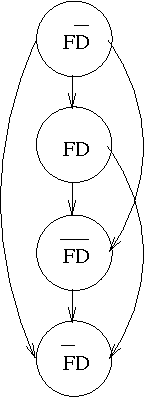
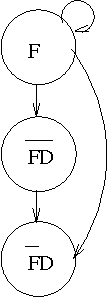
Abstract:We consider the two-fold problem of representing collective beliefs and aggregating these beliefs. We propose modular, transitive relations for collective beliefs. They allow us to represent conflicting opinions and they have a clear semantics. We compare them with the quasi-transitive relations often used in Social Choice. Then, we describe a way to construct the belief state of an agent informed by a set of sources of varying degrees of reliability. This construction circumvents Arrow's Impossibility Theorem in a satisfactory manner. Finally, we give a simple set-theory-based operator for combining the information of multiple agents. We show that this operator satisfies the desirable invariants of idempotence, commutativity, and associativity, and, thus, is well-behaved when iterated, and we describe a computationally effective way of computing the resulting belief state.
* 19 pages, 5 figures, appears (without proofs) in Proceedings of the Seventh International Conference on Principles of Knowledge Representation and Reasoning (KR 2000)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge