Representing and Aggregating Conflicting Beliefs
Paper and Code
Mar 11, 2002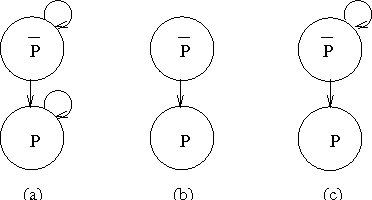
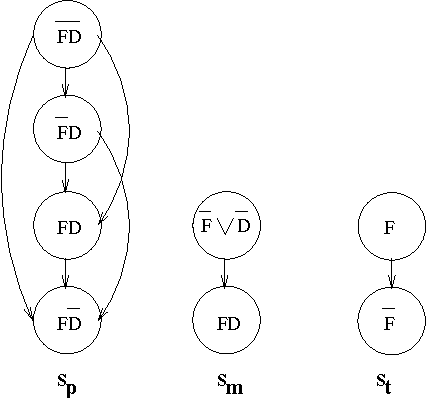
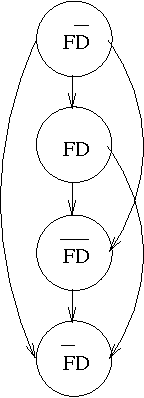
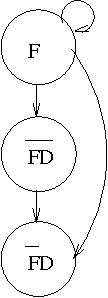
We consider the two-fold problem of representing collective beliefs and aggregating these beliefs. We propose modular, transitive relations for collective beliefs. They allow us to represent conflicting opinions and they have a clear semantics. We compare them with the quasi-transitive relations often used in Social Choice. Then, we describe a way to construct the belief state of an agent informed by a set of sources of varying degrees of reliability. This construction circumvents Arrow's Impossibility Theorem in a satisfactory manner. Finally, we give a simple set-theory-based operator for combining the information of multiple agents. We show that this operator satisfies the desirable invariants of idempotence, commutativity, and associativity, and, thus, is well-behaved when iterated, and we describe a computationally effective way of computing the resulting belief state.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge