Daniel Lehmann
Hebrew University
Generalized Qualitative Probability: Savage Revisited
Aug 07, 2014Abstract:Preferences among acts are analyzed in the style of L. Savage, but as partially ordered. The rationality postulates considered are weaker than Savage's on three counts. The Sure Thing Principle is derived in this setting. The postulates are shown to lead to a characterization of generalized qualitative probability that includes and blends both traditional qualitative probability and the ranked structures used in logical approaches.
Algebras of Measurements: the logical structure of Quantum Mechanics
Dec 08, 2005Abstract:In Quantum Physics, a measurement is represented by a projection on some closed subspace of a Hilbert space. We study algebras of operators that abstract from the algebra of projections on closed subspaces of a Hilbert space. The properties of such operators are justified on epistemological grounds. Commutation of measurements is a central topic of interest. Classical logical systems may be viewed as measurement algebras in which all measurements commute. Keywords: Quantum measurements, Measurement algebras, Quantum Logic. PACS: 02.10.-v.
* Submitted, 30 pages
Connectives in Quantum and other Cumulative Logics
Aug 02, 2002Abstract:Cumulative logics are studied in an abstract setting, i.e., without connectives, very much in the spirit of Makinson's early work. A powerful representation theorem characterizes those logics by choice functions that satisfy a weakening of Sen's property alpha, in the spirit of the author's "Nonmonotonic Logics and Semantics" (JLC). The representation results obtained are surprisingly smooth: in the completeness part the choice function may be defined on any set of worlds, not only definable sets and no definability-preservation property is required in the soundness part. For abstract cumulative logics, proper conjunction and negation may be defined. Contrary to the situation studied in "Nonmonotonic Logics and Semantics" no proper disjunction seems to be definable in general. The cumulative relations of KLM that satisfy some weakening of the consistency preservation property all define cumulative logics with a proper negation. Quantum Logics, as defined by Engesser and Gabbay are such cumulative logics but the negation defined by orthogonal complement does not provide a proper negation.
Nonmonotonic Logics and Semantics
Apr 15, 2002Abstract:Tarski gave a general semantics for deductive reasoning: a formula a may be deduced from a set A of formulas iff a holds in all models in which each of the elements of A holds. A more liberal semantics has been considered: a formula a may be deduced from a set A of formulas iff a holds in all of the "preferred" models in which all the elements of A hold. Shoham proposed that the notion of "preferred" models be defined by a partial ordering on the models of the underlying language. A more general semantics is described in this paper, based on a set of natural properties of choice functions. This semantics is here shown to be equivalent to a semantics based on comparing the relative "importance" of sets of models, by what amounts to a qualitative probability measure. The consequence operations defined by the equivalent semantics are then characterized by a weakening of Tarski's properties in which the monotonicity requirement is replaced by three weaker conditions. Classical propositional connectives are characterized by natural introduction-elimination rules in a nonmonotonic setting. Even in the nonmonotonic setting, one obtains classical propositional logic, thus showing that monotonicity is not required to justify classical propositional connectives.
* 28 pages. Misprint corrected 15/04/02
Belief Revision and Rational Inference
Apr 14, 2002Abstract:The (extended) AGM postulates for belief revision seem to deal with the revision of a given theory K by an arbitrary formula, but not to constrain the revisions of two different theories by the same formula. A new postulate is proposed and compared with other similar postulates that have been proposed in the literature. The AGM revisions that satisfy this new postulate stand in one-to-one correspondence with the rational, consistency-preserving relations. This correspondence is described explicitly. Two viewpoints on iterative revisions are distinguished and discussed.
NetNeg: A Connectionist-Agent Integrated System for Representing Musical Knowledge
Mar 17, 2002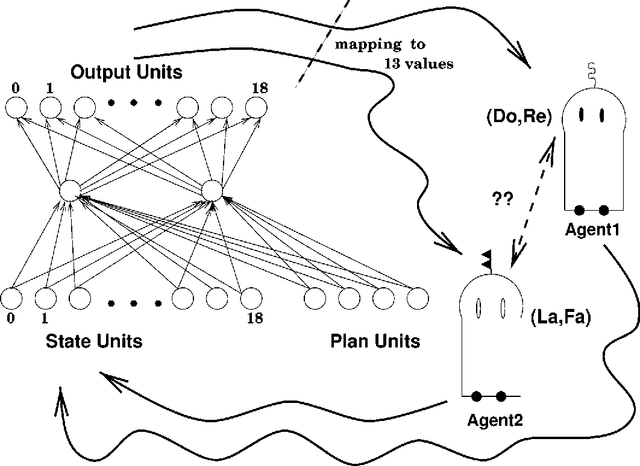


Abstract:The system presented here shows the feasibility of modeling the knowledge involved in a complex musical activity by integrating sub-symbolic and symbolic processes. This research focuses on the question of whether there is any advantage in integrating a neural network together with a distributed artificial intelligence approach within the music domain. The primary purpose of our work is to design a model that describes the different aspects a user might be interested in considering when involved in a musical activity. The approach we suggest in this work enables the musician to encode his knowledge, intuitions, and aesthetic taste into different modules. The system captures these aspects by computing and applying three distinct functions: rules, fuzzy concepts, and learning. As a case study, we began experimenting with first species two-part counterpoint melodies. We have developed a hybrid system composed of a connectionist module and an agent-based module to combine the sub-symbolic and symbolic levels to achieve this task. The technique presented here to represent musical knowledge constitutes a new approach for composing polyphonic music.
* 21 pages, 3 figures, Preliminary versions presented at International Computer Music Conference, pp. 133-140, Hong Kong (China), August 1996 and AAAI Spring Symposium, 1999
Representing and Aggregating Conflicting Beliefs
Mar 11, 2002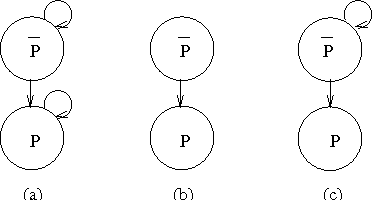
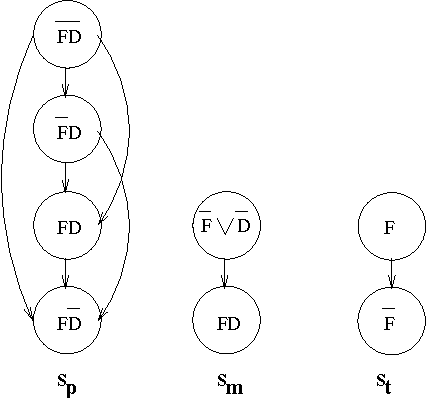
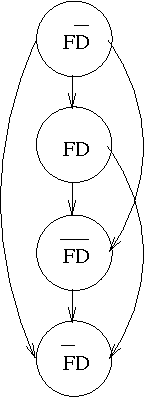
Abstract:We consider the two-fold problem of representing collective beliefs and aggregating these beliefs. We propose modular, transitive relations for collective beliefs. They allow us to represent conflicting opinions and they have a clear semantics. We compare them with the quasi-transitive relations often used in Social Choice. Then, we describe a way to construct the belief state of an agent informed by a set of sources of varying degrees of reliability. This construction circumvents Arrow's Impossibility Theorem in a satisfactory manner. Finally, we give a simple set-theory-based operator for combining the information of multiple agents. We show that this operator satisfies the desirable invariants of idempotence, commutativity, and associativity, and, thus, is well-behaved when iterated, and we describe a computationally effective way of computing the resulting belief state.
* 19 pages, 5 figures, appears (without proofs) in Proceedings of the Seventh International Conference on Principles of Knowledge Representation and Reasoning (KR 2000)
Stereotypical Reasoning: Logical Properties
Mar 04, 2002Abstract:Stereotypical reasoning assumes that the situation at hand is one of a kind and that it enjoys the properties generally associated with that kind of situation. It is one of the most basic forms of nonmonotonic reasoning. A formal model for stereotypical reasoning is proposed and the logical properties of this form of reasoning are studied. Stereotypical reasoning is shown to be cumulative under weak assumptions.
* Presented at Fourth Workshop on Logic, Language, Information and Computation, Fortaleza (Brasil), August 1997
Deductive Nonmonotonic Inference Operations: Antitonic Representations
Mar 01, 2002Abstract:We provide a characterization of those nonmonotonic inference operations C for which C(X) may be described as the set of all logical consequences of X together with some set of additional assumptions S(X) that depends anti-monotonically on X (i.e., X is a subset of Y implies that S(Y) is a subset of S(X)). The operations represented are exactly characterized in terms of properties most of which have been studied in Freund-Lehmann(cs.AI/0202031). Similar characterizations of right-absorbing and cumulative operations are also provided. For cumulative operations, our results fit in closely with those of Freund. We then discuss extending finitary operations to infinitary operations in a canonical way and discuss co-compactness properties. Our results provide a satisfactory notion of pseudo-compactness, generalizing to deductive nonmonotonic operations the notion of compactness for monotonic operations. They also provide an alternative, more elegant and more general, proof of the existence of an infinitary deductive extension for any finitary deductive operation (Theorem 7.9 of Freund-Lehmann).
Another perspective on Default Reasoning
Mar 01, 2002Abstract:The lexicographic closure of any given finite set D of normal defaults is defined. A conditional assertion "if a then b" is in this lexicographic closure if, given the defaults D and the fact a, one would conclude b. The lexicographic closure is essentially a rational extension of D, and of its rational closure, defined in a previous paper. It provides a logic of normal defaults that is different from the one proposed by R. Reiter and that is rich enough not to require the consideration of non-normal defaults. A large number of examples are provided to show that the lexicographic closure corresponds to the basic intuitions behind Reiter's logic of defaults.
* Presented at Workshop on Logical Formalizations of Commense Sense, Austin (Texas), January 1993
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge