The Equational Approach to CF2 Semantics

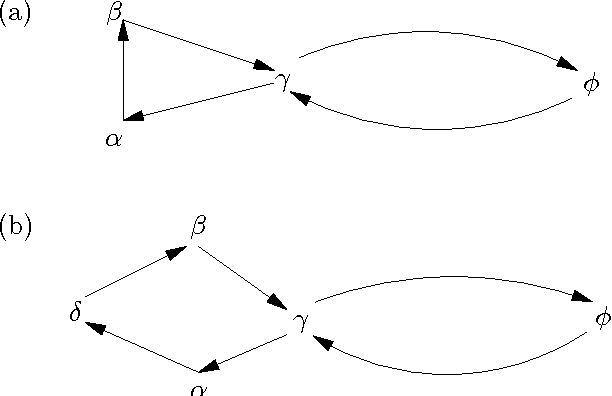
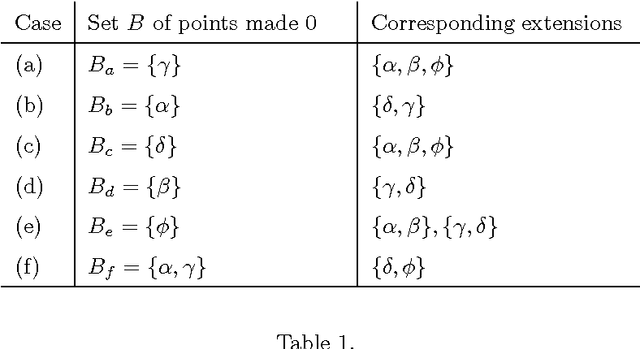
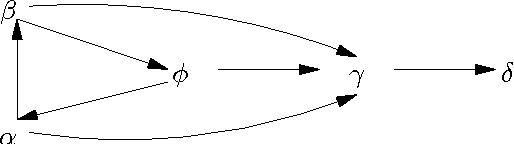
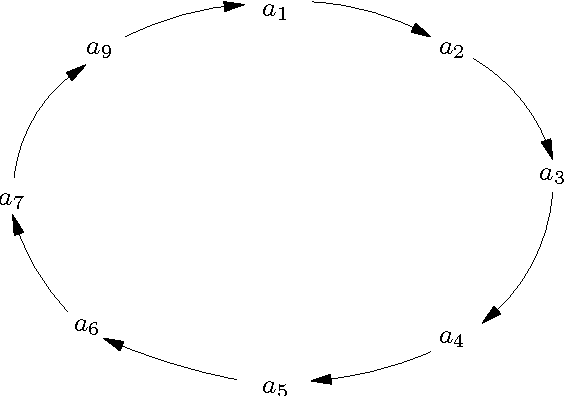
We introduce a family of new equational semantics for argumentation networks which can handle odd and even loops in a uniform manner. We offer one version of equational semantics which is equivalent to CF2 semantics, and a better version which gives the same results as traditional Dung semantics for even loops but can still handle odd loops.

Algebras of Measurements: the logical structure of Quantum Mechanics

In Quantum Physics, a measurement is represented by a projection on some closed subspace of a Hilbert space. We study algebras of operators that abstract from the algebra of projections on closed subspaces of a Hilbert space. The properties of such operators are justified on epistemological grounds. Commutation of measurements is a central topic of interest. Classical logical systems may be viewed as measurement algebras in which all measurements commute. Keywords: Quantum measurements, Measurement algebras, Quantum Logic. PACS: 02.10.-v.