Neural Likelihoods via Cumulative Distribution Functions

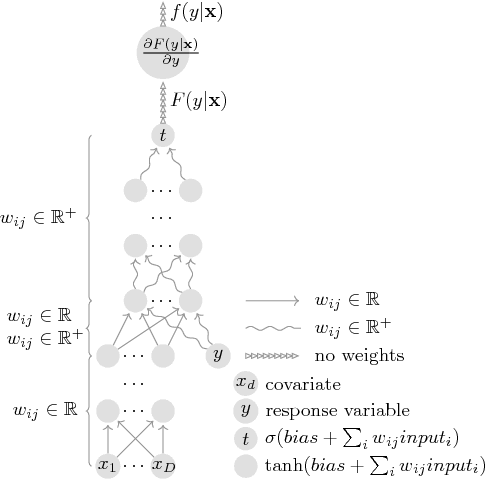
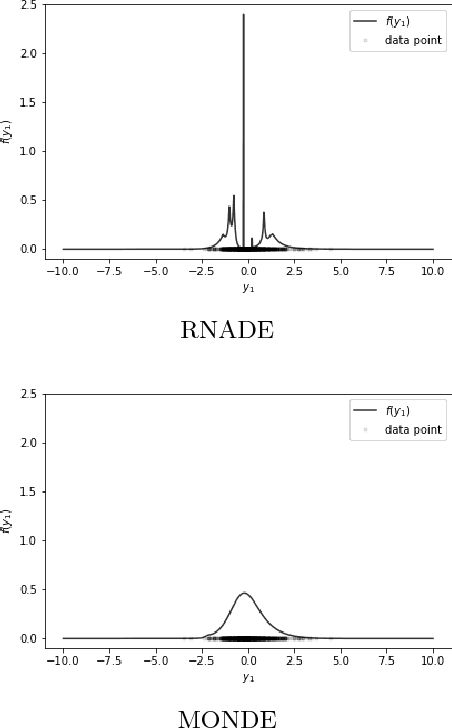
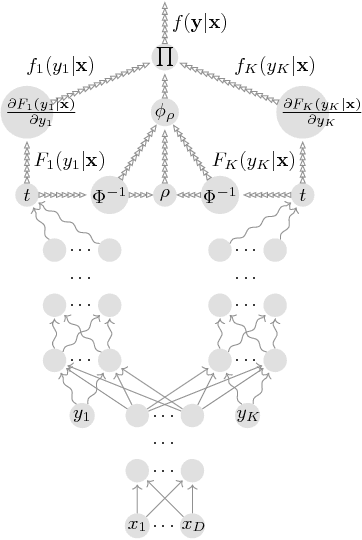
We leverage neural networks as universal approximators of monotonic functions to build a parameterization of conditional cumulative distribution functions. By a modification of backpropagation as applied both to parameters and outputs, we show that we are able to build black box density estimators which are competitive against recently proposed models, while avoiding assumptions concerning the base distribution in a mixture model. That is, it makes no use of parametric models as building blocks. This approach removes some undesirable degrees of freedom on the design on neural networks for flexible conditional density estimation, while implementation can be easily accomplished by standard algorithms readily available in popular neural network toolboxes.

Scaling Factorial Hidden Markov Models: Stochastic Variational Inference without Messages

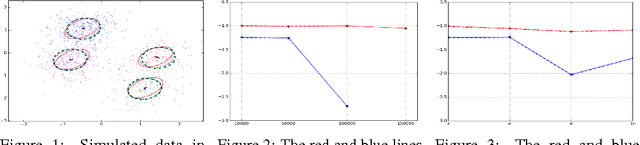
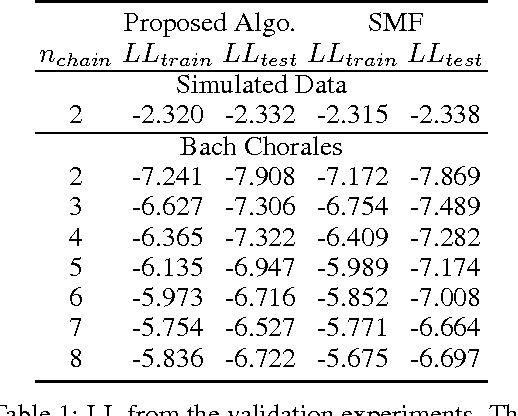
Factorial Hidden Markov Models (FHMMs) are powerful models for sequential data but they do not scale well with long sequences. We propose a scalable inference and learning algorithm for FHMMs that draws on ideas from the stochastic variational inference, neural network and copula literatures. Unlike existing approaches, the proposed algorithm requires no message passing procedure among latent variables and can be distributed to a network of computers to speed up learning. Our experiments corroborate that the proposed algorithm does not introduce further approximation bias compared to the proven structured mean-field algorithm, and achieves better performance with long sequences and large FHMMs.